Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.1 - Ex. 10
Seja
a) Mostre que é inversível e determine sua inversa
b) Esboce os gráficos de e de
Passo 1
a) Para saber se a função é invertível precisamos saber se ela é bijetora.
E ela ser bijetora é cada elemento do domínio se relacionar com somente um elemento da imagem e vice versa.
Repara que o domínio é o conjunto dos números reais (porque podemos jogar qualquer número no x).
E a imagem também vai ser o conjunto do reais (substitui ali “infinito” que a gente acha infinito e “-intinto” que a gente acha menos infinito).
E a função é bijetora porque todos os x que a gente colocar vai dar um y diferente. Repara que se a gente substituir, intuitivamente o x por -x (pra ver se vai dar valor de y diferente mesmo), ficamos com:
E realmente é diferente.
Então a gente escreve assim:
“Como a função é bijetora e essa é uma condição necessária e suficiente para ser inversível, então é inversível.”
Escrevemos para obter a inversa :
Multiplicamos toda a equação por :
Passo 2
Veja que chegamos a uma equação do segundo grau na variável . Resolvendo, obtemos:
Como é sempre positivo, desprezamos a solução negativa, restando apenas:
E assim,
Passo 3
b) Agora vamos esboçar os gráficos, com em vermelho e em azul:
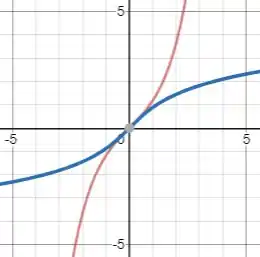
Repare que os gráficos são simétricos em relação à reta , pois uma função é inversa da outra!
Resposta
a)