Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.3 - Ex. 66
66. Seja , onde é a função cujo gráfico é mostrado. Onde é côncava para baixo?
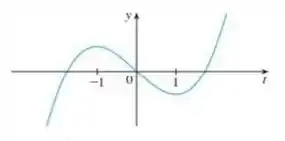
Passo 1
Fala aí! tudo certinho?
Nesse caso foi dada a função:
Onde é dada pela curva:
A partir daí, queremos estimar o intervalo onde tem concavidade para baixo.
Tem ideia de como fazemos isso?
Lembra que a concavidade de uma função é interpretada como a derivada de segunda ordem dessa função? Então... para responder essa questão vamos usar esse teorema.
A concavidade da função está diretamente ligada ao sinal de , então se a concavidade é para cima e quando a concavidade de é para cima.
No caso a nossa função é , aplicando o TFC, descobrimos que a primeira deriva é:
Onde seu gráfico é dado pelo gráfico do enunciado. Com isso, a segunda derivada de pode ser interpretada como a primeira derivada de .
Ou seja, a inclinação de está diretamente relacionada à concavidade de .
Veja só!
Passo 2
Saca só, a gente sabe que a derivada vai ser positiva se caso a inclinação da reta for positiva, e ela será negativa se caso a inclinação da reta também for negativa.
Podemos separar dentro do gráfico desse jeito
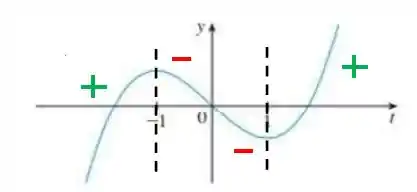
Portanto, podemos definir os intervalos de concavidade para cima como:
E o intervalo de concavidade para baixo é:
É isso! Entendeu tudo? Responde Aí!
Resposta
Os intervalos de concavidade para cima são:
E o intervalo de concavidade para baixo é: