Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.2 - Ex. 4
4 ) Seja , onde f (x, y) = x + 2y. Desenhe F(x, y), com (x, y)na reta x + 2y = 1.
Passo 1
Queremos o campo vetorial do Gradiente de . Sabendo que . E que o cálculo de gradiente é
Podemos dizer que ,
Passo 2
Abaixo podemos ver esse campo geometricamente ao longo da reta
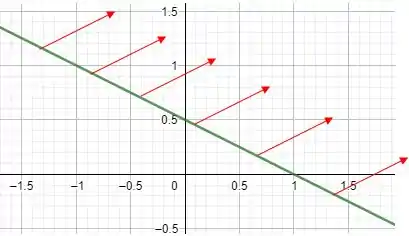
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine uma função f tal que F = ∇ f e (b) use a parte (a) para calcular ∫ c F → ⋅ d r → sobre a curva C dada. F x , y , z = s e nyi ^ + x cos y + cos z j ^ - ys e nzk ^ C : r → t = s e nti ^ +
Determine uma função f tal que F = ∇ f e (b) use a parte (a) para calcular ∫ c F → ⋅ d r → sobre a curva C dada. F x , y , z = y z e x zi ^ + e x z j ^ + x y e x zk ^ C : r → t = ( t 2 + 1 )i ^ + ( t
Determine se o conjunto dado é ou não: (a) aberto, (b) conexo por caminhos e (c) simplesmente conexo. x , y1 ≤ x 2 + y 2 ≤ 4 ,y ≥ 0
Determine se o conjunto dado é ou não: (a) aberto, (b) conexo por caminhos e (c) simplesmente conexo. x , y x , y ≠ 2,3