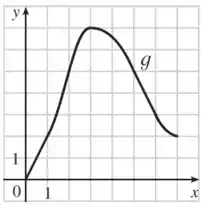
Seja onde é a função cujo gráfico é mostrado.
(a) Calcule , , , e
(b) Em que intervalos está crescendo?
(c) Onde tem um valor máximo?
(d) Faça um esboço do gráfico de .
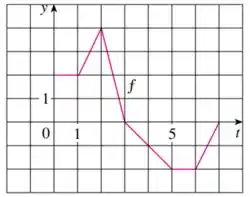
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte gráfico de :
Ele também nos diz que
Queremos calcular para .
Para isso, devemos substituir na função dada e analisar o gráfico para podermos encontrar os valores dentro de cada intervalo.
Assim, lembre-se que a integral pode ser interpretada como a área sob a curva, e é isso que vamos usar aqui para o item A.
Para o B iremos ver quais a função cresce, ou seja, para quais intervalos nosso gráfico aponta para cima.
O valor máximo será o onde a função é mais alta
Com isso, poderemos analisar onde está crescendo e o seu valor de máximo.
E para esboço, vamos analisar as informações que respondemos nos itens anteriores, ok?
Um bocadinho de coisa, né?? Mas vamos devagarinho que vai dar certo!! 😉
Passo 2
Item a:
Se
e essa integral é a área do gráfico, então:
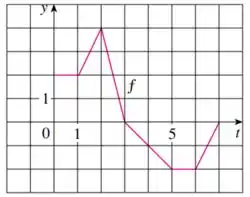
Para , temos:
0
Observe no gráfico como não temos área, essa região é apenas uma linha:

Para , temos a área de dois quadrados de lado , logo:
Agora sim temos uma área no gráfico, observe como há quadradinhos de área no intervalo
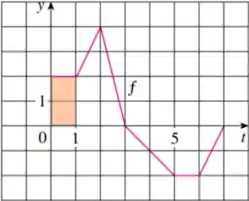
Para :
Já sabemos área no intervalo de , vamos observar a área dos intervalos de, nossa área total quando x=2, é a soma das áreas laranja e vermelha, desse jeito:
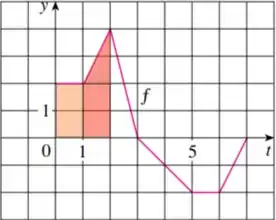
Para a integral de intervalo , perceba no gráfico que se trata da área de dois quadrados de lado e um triângulo de base e altura , portanto, vamos somar essa área com a que já temos:
Para , temos:
Perceba que já sabemos do resultado da integral de .
Por outro lado, para a integral de intervalo , perceba no gráfico que se trata da área de um triângulo de base e altura , aqui será a nossa área em azul, portanto:
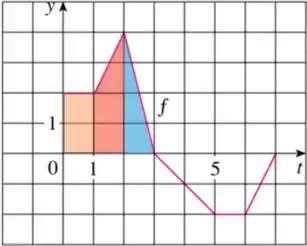
Para , temos:
Perceba que já sabemos do resultado da integral de . Então precisamos somar com a área verde que vai de a .
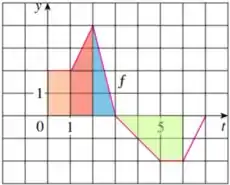
Para a integral de intervalo , perceba no gráfico que se trata da área de um trapézio (do lado negativo) de base maior , base menor e altura , e note que agora vamos subtrair essa área, pois está abaixo do :
Passo 3
Item b:
Como estamos ampliando a área positiva até , então a função está crescendo até , pois que é a derivada de tem valores positivos!
Passo 4
Item c:
Até nosso gráfico estava acima do , após ele ficou abaixo. Isso quer dizer que até as derivadas de eram positivas, e após elas ficaram negativas, indicando aqui um ponto de mudança de sentido da função, se você pensou em uma curva, acertou! E mais um detalhe, lembre-se que no ponto máximo ou mínimo que é exatamente o que temos!
Passo 5
Item d:
Temos então o esboço:
- A função começa em
- Ela cresce até , onde tem seu ponto máximo
- Após ela decresce
Juntando todas essas informações conseguimos plotar um esboço!
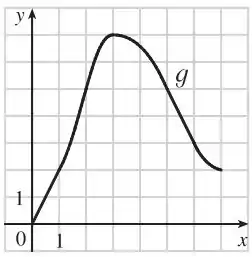
Curtiu? Responde Aí!
Resposta
(a) , , , , .
(b) A função está crescendo até .
(c) é o máximo de .
(d)