Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.3 - Ex. 3

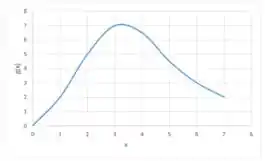
Seja g x = ∫ 0 x f t   d t onde f é a função cujo gráfico é mostrado.

(a) Calcule g 0 , g 1 , g 2 , g 3 e g 6 .

(b) Em que intervalos g está crescendo?

(c) Onde g tem um valor máximo?

(d) Faça um esboço do gráfico de g .

Passo 1

Fala aí! tudo certinho?

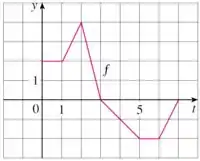
Nesse problema foi dado um gráfico de uma função f t :

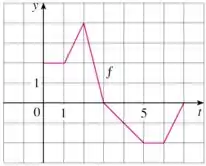
E foi dado também que g x = ∫ 0 x f t   d t .

A partir daí queremos calcular g 0 , g 1 , g 2 , g 3 e g 6 , determinar o intervalo onde g é crescente e seu ponto máximo.

Além disso queremos fazer um esboço de g .

Bastante coisa, não é?

Para responder essa questão temos que lembrar que a integral de uma função pode ser interpretada como a área abaixo da curva dessa função.

Então como:

g x = ∫ 0 x f t   d t

Para determinar os valores de g , substituímos x = a e calculamos a área abaixo da curva f no intervalo 0 , a .

A partir daí podemos determinar o intervalo onde a função g é crescente, também seu ponto máximo e esboçar seu gráfico.

Bora começar!

Passo 2

Começando com g ( 0 ) . Para x = 0 , temos:

g 0 = ∫ 0 0 f t   d t = 0

Aqui não tem erro, os limites de integração são iguais então a integral é nula.

Para x = 1 , temos:

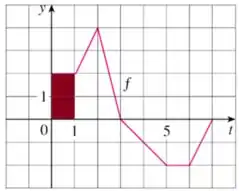
Dessa forma o valor de g 1 pode ser interpretado como a área do retângulo de base 1 e altura 2 .

g 1 = 1 · 2 = 2

Para g ( 2 ) temos:

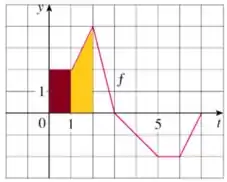
Podemos interpretar g 2 como:

g 2 = ∫ 0 2 f t   d t = ∫ 0 1 f t   d t + ∫ 1 2 f t   d t

g 2 = g 1 + ∫ 1 2 f t   d t

Já temos o valor de g 1 e ∫ 1 2 f t   d t é dado pela áreas do trapézio amarelo de base maior 4 , base menor 2 e altura 1 .

g 2 = 2 + 4 + 2 1 2

g 2 = 5

Tranquilo até aqui?

Passo 3

Agora para x = 3 , temos:

g 3 = ∫ 0 3 f t   d t = ∫ 0 2 f t   d t + ∫ 2 3 f t   d t

g 3 = g 2 + ∫ 2 3 f t �� d t

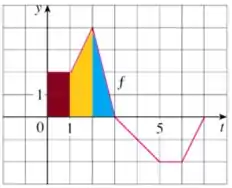
Temos o valor de g 2 e ∫ 2 3 f t   d t é dado pela área do triângulo de base 1 e altura 4 .

g 3 = 5 + 1 · 4 2

g 3 = 7

Por fim, queremos g 6 :

g 6 = ∫ 0 6 f t   d t = ∫ 0 3 f t   d t + ∫ 3 6 f t   d t

g 6 = g 3 + ∫ 3 6 f t   d t

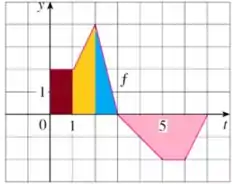
Mais uma vez temos o valor de g 3 e podemos interpretar a região entre x = 3 e x = 6 como um trapézio de base maior 4 , base menor 1 e altura 2 .

Porém perceba que essa área está abaixo do eixo x , portanto, é negativa.

g 6 = 7 - 3 + 1 2 2

g 6 = 3

Show?

Passo 4

A letra (b) pergunta em que intervalos g está crescendo! Vamos trazer o gráfico pra pertinho da gente:

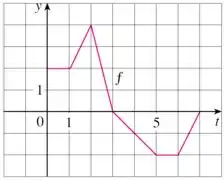
Se g está diretamente ligada à área abaixo de f , podemos dizer que g é crescente quando a área abaixo de f é positiva.

Portanto, a função g x é crescente no intervalo:

0 ≤ x ≤ 3

Maravilha!

Passo 5

A letra (c) pergunta onde g tem um valor máximo, lembrando que g ( x ) é uma integral:

g x = ∫ 0 x f t   d t

De x = 0 até  x = 3 ela sempre cresce e depois começa a decrescer. Dessa forma o valor máximo se da em g ( 3 ) .

g 3 = 7

Estamos quase no fim!

Passo 6

Pra acabar, precisamos fazer um esboço do gráfico de g , para isso vamos pegar os valores calculados na letra (a) e calcular g ( 4 ) , g 5 e g ( 7 ) .

Vamos fazer da mesma forma que fizemos nos passos 2 e 3...

g 4 = g 3 + - 1 × 1 2 = 13 2

g 5 = g 4 + - 2 × 2 2 = 9 2

g 7 = g 6 + - 1 × 2 2 = 2

Assim, esboçando a curva de g x a partir dos valores de g que calculamos, vamos obter:

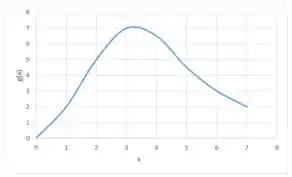
É isso! O que achou? Responde Aí!

Resposta

(a) g 0 = 0 , g 1 = 2 , g 2 = 5 , g 3 = 7 , g 6 = 3 .

(b) A função está crescendo até x = 3 .

(c) x = 3 é o máximo de g .

(d) Esboço da curva.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.Num tanque d’água cilíndrico (com eixo vertical), a força do fluido na base do tanque é igual ao peso da água no tanque.
Nestes exercícios, quando necessário, consulte a Tabela 6.8.2 para os pesos específicos dos fluidos.(b) Encontre a força (em l b ) sobre a máscara de um mergulhador se sua área for de 60p o l 2 e a pr
Num tanque d’água retangular, a força do fluido em qualquer um dos lados do tanque é menor do que a força do fluido na base do tanque.
Nestes exercícios, quando necessário, consulte a Tabela 6.8.2 para os pesos específicos dos fluidos.Uma placa retangular plana é imersa horizontalmente em água.(a) Encontre a força (em l b ) e a press
As superfícies planas mostradas estão imersas verticalmente em água. Encontre a força do fluido sobre cada superfície.