Um tanque de óleo tem a forma de um cilindro circular reto, com de diâmetro. Encontre a força total do fluido sobre um extremo quando o eixo é horizontal e o tanque está cheio até a metade com um óleo de peso específico de .

Para achar , que é a largura da nossa região que varia com a profundidade , vamos ter que usar nossa esperteza. Vamos considerar que a origem do eixo está na altura da superfície do líquido.

Olha essa figura:

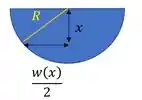
Esse desenho mostra que a metade da largura da placa, o raio do semicírculo e o valor de fazem um triângulo retângulo. A gente pode usar nosso amigo, o Teorema de Pitágoras:

Porque o raio vale . Isolando :

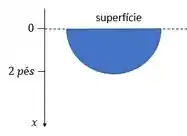
Já a profundidade, vemos que é medida diretamente pelo valor de . Então, podemos escrever:

E a placa começa em e termina em .

Com tudo isso, nossa integral fica assim:

Agora é só calcular a integral. Usando a substituição:

Nossos extremos de integração ficam assim:

E a integral fica desse jeitinho: