Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.8 - Ex. 3

As superfícies planas mostradas estão imersas verticalmente em água. Encontre a força do fluido sobre cada superfície.

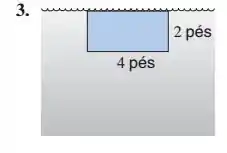
Passo 1

Como temos uma placa submersa na vertical, podemos usar essa relação:

Onde é o peso específico da água. Precisamos usar o que está na nossa tabelinha e está nas mesmas unidades do enunciado:

E é a largura da placa e a profundidade de cada ponto . (sendo e os limites da placa nessa profundidade).

E sendo o eixo , um eixo vertical para baixo, com a origem () na superfície do líquido.

Vamos começar!

Passo 2

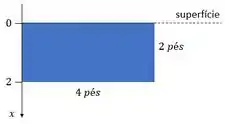
Pela figura vemos que a largura é constante e igual a:

Vemos que a profundidade é medida diretamente pelo valor de . Então, podemos escrever:

E a placa começa em e termina em .

Com tudo isso, nossa integral fica assim:

Passo 3

Agora é só calcular a integral:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a definição 5.5 . 1 para expressar as integrais como limites de somas de Riemann. (não calcule as integrais.) ∫ 1 2 xd x ∫ - π 2 π 2 1 + cos ⁡ x d x

Use os valores dados de aeb para expressar os limites seguintes como integrais. (não calcule as integrais) lim max ⁡ Δ x k → 0 ⁡ ∑ k = 1 n 4 x k * 1 - 3 x k * Δ x k ;a = - 3 ,b = 3

Explique informalmente por que o Teorema 5.5 . 4a decorre da Definição 5.5 . 1 .

Esboce a região cuja área com sinal é representada pela integral definida e calcule a integral usando uma fórmula apropriada de Geometria quando for necessário. a )∫ 0 5 2d x c )∫ - 1 2 | 2 x - 3 | d

Explique informalmente por que o Teorema 5.5 . 6a decorre da Definição 5.5 . 1 .