Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.7 - Ex. 9
9. Seja D a região do plano xy limitada pelas circunferências e de equações
E
Respectivamente. Se e são de classe em D e em D. Quais os possíveis valores da integral
Onde C é uma curva qualquer fechada contida em D, C¹ por partes, sabendo -se que
Quando e estao orientadas no sentido anti-horario. Justifique sua resposta
Passo 1
Oii, estamos ingressando no mundo dos teoremas de integração de cálculo. E nessa parte da matéria temos que aprender que existem muitas respostas diferentes utilizando caminhos diferentes como é neste caso de integração de linha. OU várias formas de se calcular que geram o mesmo resultado!
Sim, você ouviu certo. Vão ter contas que podemos fazer por ate 3 caminhos diferentes. Então a pergunta é : qual escolher? Segue vendo as nossas resoluções que vamos te dar umas dicas.
Passo 2
Neste capítulo trabalhamos conceitos de funções vetoriais, Teorema de Green e Campo conservativo. Vamos ter que lançar mãos de tudo isso para resolver nossas questões. Bora fazer uma revisão de leve nos teoremas. O Teorema de Green diz
Outra forma de enxergar seria
Quando nosso campo é conservativo, acontece que
Podemos fazer o rotacional e descobrir isso, ou por uma simples propriedade de diferenciação saber que
e quando o nosso campo é conservativo podemos dizer que existe uma função Potencial U, de forma que
Beleza? É bom fazer essa revisãozinha pra a gente já chegar afiado nas questões!!!!
Passo 3
Nesta questão temos que nossa região é
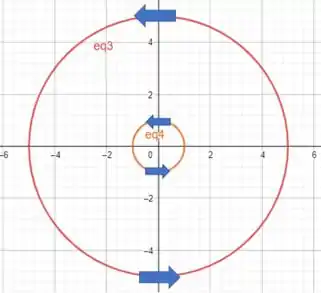
O espaço entre as duas equações e como elas tem a mesma orientação
Agora a solução é feita por um argumento geométrico. Se pegarmos uma curva qualquer entre esses dois círculos teremos
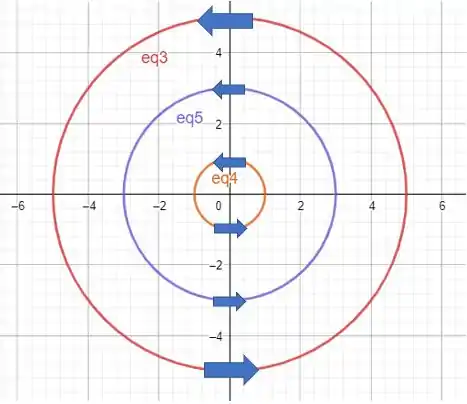
OU seja essa curva C3 como esta na mesma orientação que as outras duas logo
Agora se eu orientar de forma contraria, logo o sinal do nosso resultado sera trocado
Passo 4
Agora se eu pegar uma curva qualquer dentro da nossa região
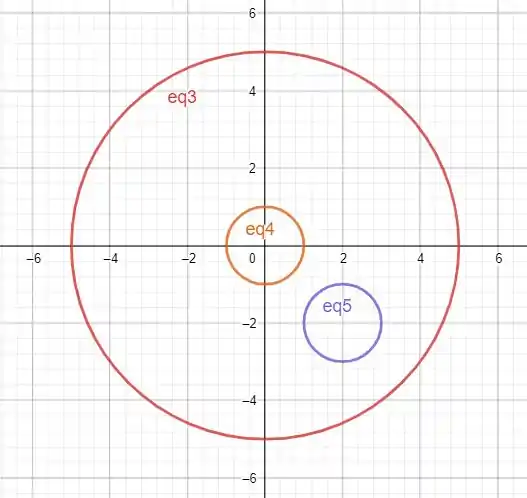
Entao teríamos que aplicar o teorema de green
E como o enunciado diz
Logo essa curva teria valor nulo
Terminamos por aqui. Pode comemorar! \o/
Te vejo na próxima resolução
: )