Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.7 - Ex. 8
8. Sejam e funções reais de classe em (A e B como na figura 6.18) tais que
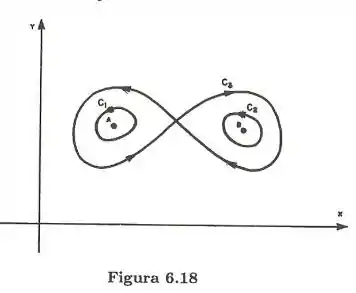
Em U. Sendo as curvas dadas na figura 6.18. Calcule
Supondo que
E
Passo 1
Oii, estamos ingressando no mundo dos teoremas de integração de cálculo. E nessa parte da matéria temos que aprender que existem muitas respostas diferentes utilizando caminhos diferentes como é neste caso de integração de linha. OU várias formas de se calcular que geram o mesmo resultado!
Sim, você ouviu certo. Vão ter contas que podemos fazer por ate 3 caminhos diferentes. Então a pergunta é : qual escolher? Segue vendo as nossas resoluções que vamos te dar umas dicas.
Passo 2
Neste capítulo trabalhamos conceitos de funções vetoriais, Teorema de Green e Campo conservativo. Vamos ter que lançar mãos de tudo isso para resolver nossas questões. Bora fazer uma revisão de leve nos teoremas. O Teorema de Green diz
Outra forma de enxergar seria
Quando nosso campo é conservativo, acontece que
Podemos fazer o rotacional e descobrir isso, ou por uma simples propriedade de diferenciação saber que
e quando o nosso campo é conservativo podemos dizer que existe uma função Potencial U, de forma que
Beleza? É bom fazer essa revisãozinha pra a gente já chegar afiado nas questões!!!!
Passo 3
Nesta questão temos
Porque podemos falar isso? Simples
Então as integrais teriam que zerar em todo o domínio. Contudo
Não funciona nos pontos A e B. Assim reduzimos a calcular o fluxo que escapa nesses pontos. Agora beleza, como sabemos que um soma e outro diminui? A orientação das curvas nos dá essa dica. C1 está com a mesma orientação que C3, já C2 está com uma orientação contraria.
Terminamos por aqui. Pode comemorar! \o/
Te vejo na próxima resolução
: )