Seja σ : K → R 3 regular no interior de K e injetora em K ; suponha que as componentes de σ ,x = x u , v , y = y u , v e z = z u , v , sejam de classe C 2 num aberto contendo K . Suponha que K tenha a forma abaixo, onde γ 1 : a 1 , b 1 → R 2 e γ 2 : a 2 , b 2 → R 2 são curvas simples, fechadas, C 1 por partes, sendo γ 1 orientada no sentido anti-horário e γ 2 no sentido horário e tais que a fronteira de K é igual a I mγ 1 ∪ I mγ 2 . Sejam Γ 1 t = σ γ 1 t ,t ∈ a 1 , b 1 , e Γ 2 t = σ γ 2 t , t ∈ a 2 , b 2 .Seja F → = Pi → + Qj → + Rk → de classe C 1 num aberto contendo I mσ e seja n → = ∂ σ ∂ u ∧ ∂ σ ∂ v ∂ σ ∂ u ∧ ∂ σ ∂ v Prove que ∬ σ r o tF → ⋅ n →d S = ∫ Γ 1 F → ⋅ d r → + ∫ Γ 2 F → ⋅ d r →

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 3

Seja regular no interior de e injetora em ; suponha que as componentes de e , sejam de classe num aberto contendo . Suponha que tenha a forma abaixo, onde

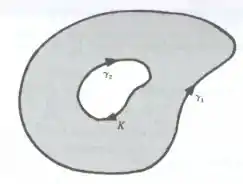
e são curvas simples, fechadas, por partes, sendo orientada no sentido anti-horário e no sentido horário e tais que a fronteira de é igual a . Sejam , e .

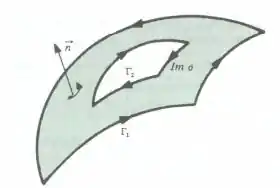
Seja de classe num aberto contendo e seja

Prove que

Passo 1

Do Teorema de Stokes temos que dado um uma porção de superfície regular com parametrização definida por e que são supostas de classe num aberto contendo e tendo um campo vetorial de classe num aberto que contém , então teremo que

Na qual é uma curva fronteira de orientada positivamente em relação a normal .

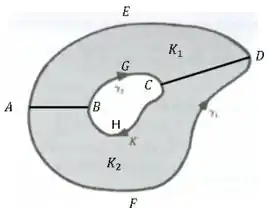
Assim vamos tomar nossos conjuntos a baixo.

Passo 2

Perceba que iremos fazer apenas um passo do nosso problema, e todo o resto já estará praticamente resolvido.

Tome a primeira imagem e vamos mostrar que

Assim tomemos que

Somando as duas equações, temos que

Logo só nos sobram

Assim temos que

Passo 3

Desta forma podemos então aplicar nosso teorema de Stokes (olhar pagina 253 da Ed)

Desta forma segue o mesmo passo que foi realizado no passo 2, mas agora indicando que estamos lidando com a segunda imagem, relativa a

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. j )F → x , y , z = y i → + x j → + x z k → ,σ é a superfície z = x + y + 2ex 2 + y 2 4

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. c )F → x , y , z = y i → + x 2 j → + z k → ,σ u , v = u , v ,2 u + v + 1 ,c o mu ≥ 0eu

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. b )F → x , y , z = y i → - x 2 j → + 5 k → ,σ u , v = u , v , 1 - u 2 , c o mu ≥ 0 ,v ≥

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. d )F → x , y , z = y i → + x 2 j → + z k → ,σ é a superfície x 2 + y 2 = 1 ,0z1 ,ey ≥0

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. f )F → x , y , z = y i → ,σ é a superfície z =x 2 + y 2c o mz ≤ 1 sendo n → a normal co