Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 20

Seja uma reta que passa pelo ponto formando um triangulo com os eixos coordenados positivos. Qual a equação de para que essa área seja mínima.

Passo 1

A ideia nessa questão será equacionar a reta passando pelo ponto . Em seguida, vamos fazer as interseções com os eixos coordenados e achar a área. Por último, minimizaremos essa área. Vem comigo!

Vamos supor que o coeficiente angular da reta seja . Assim, podemos escrever a reta da seguinte maneira:

Assim,

Passo 2

Agora vamos achar as interseções com os eixos coordenados.

Quando :

Isto é,

Quando :

Logo,

Fazendo uma ilustração:

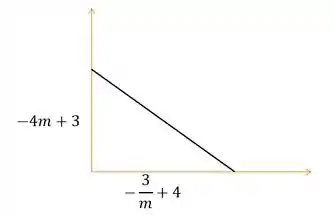
Então a área do triangulo fica o seguinte:

Fazendo a distributiva:

Passo 3

Agora vamos derivar e igualar a zero para ver os pontos críticos. A área à é o seguinte:

Derivando,

Igualando a zero:

Logo,

Tirando a raiz:

Mas repare que pela ilustração do Passo 2 a reta deve ter coeficiente angular negativo. Assim,

Substituindo esse valor de na equação do Passo 1:

Fazendo as contas:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os pontos críticos da função dada e classifique-os (a classificação refere-se a ponto de máximo local, ponto de mínimo local ou ponto de inflexão).d) f x = 1 x 4 + 2 x 3 + x 2 + 1

Determine os valores máximos e mínimos (caso existam) da função dada, no intervalo dado. f x = sen ⁡ x - cos ⁡ x em [ 0 ,π ]

Determine os valores máximos e mínimos (caso existam) da função dada, no intervalo dado. f x = x 3 - 2 x 2 3 em [ - 1 ,2 ]

Determine os valores máximos e mínimos (caso existam) da função dada, no intervalo dado. g x = x 3 - 3 x 2 + 3 x - 1 em [ - 2 ,1 ]

Determine os valores máximos e mínimos (caso existam) da função dada, no intervalo dado. f x = x 5 5 - x 4 2 - x 3 + 4 x 2 - 4 x + 1 em [ - 3 ,3 ]