Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.5 - Ex. 6
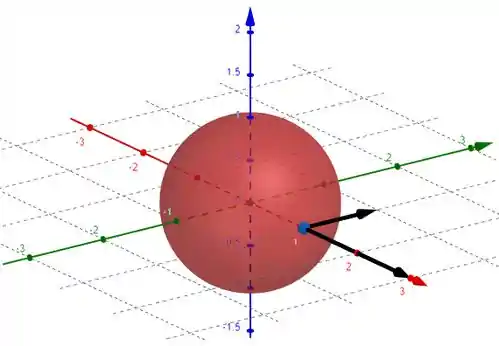
Seja e seja uma curva diferenciável cuja imagem está contida na superfície de nível . Seja . Prove que . Interprete geometricamente.
Passo 1
A curva é definida dentro da superfície de nível que é a esfera unitária.
Como a curva está contida na esfera, é sempre tangente à esfera.
O gradiente de é definido como
Que são justamente os coeficientes do plano tangente a superfície de nível , ou seja, é sempre um vetor normal à superfície de nível.
Como é tangente à esfera e é normal, se pegarmos um ponto , tal que , podemos afirmar que
Passo 2
Vamos utilizar um exemplo, a circunferência unitária é uma curva pertencente a esfera e pode ser parametrizada como .
Derivando
E o gradiente de
E o gradiente é dado por
No ponto temos , mas sabemos que , então
Na derivada , quando
E o gradiente no ponto
Calculando então o produto escalar
E de fato os vetores são perpendiculares.
Passo 3
Usando nosso exemplo para a representação geométrica, no ponto , a derivada e o gradiente :
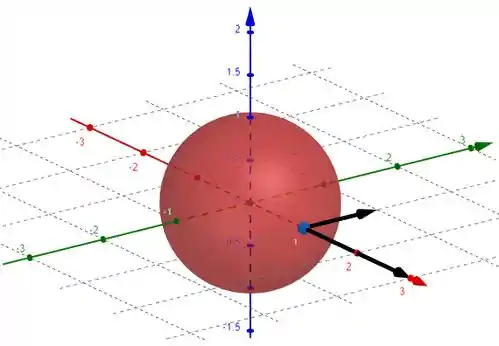
Resposta
