Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 1
Seja a superfície que é fronteira da caixa delimitada pelos planos . Aproxime usando uma soma de Riemann, como na Definição , tomando os retalhos como os retângulos que são as faces da caixa e os pontos como os centros destes retângulos.
Passo 1
A caixa é um cubo onde cada face tem área igual a unidades quadradas. O centro das faces é . Para cada face, pegamos um ponto para ser o centro da face e . Assim, pela Definição da teroia
Passo 2
Vamos escrever a integral como uma soma de Riemann!
Vamos avaliar os valores na tabela abaixo!
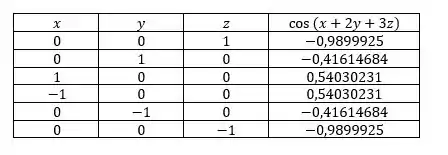
Substituindo os valores, temos:
Resposta
A integral é igual a
Exercícios de Livros Relacionados
Dada a equação vetorial ru , v = u cos v ,us e nv , u ² ² b) fazer esboço e indicar o significado geométrico dos parâmetros u e vc) determinar a área da parte da superfície que esta entre os planos
Considerando que a superfície S é obtida girando a curva z = x 2 , 0 ≤ x ≤ 4 , em torno do eixo z , pede-seUma parametrização para S .
Calcule a área das seguintes superfíciesb) Superfície do cone z 2 = x 2 + y 2 situada entre os planos z = 0 e x + 2 z = 3 .
Considere γ o arco da parábola z = 3 - y 2 no plano y z compreendido entre as semi-retas z = z = 2 y e z = 11 2 y , com y ≥ 0 . Seja S a superfície obtida girando-se γ em torno do eixo z . Pede-se:b)
Considerando que a superfície S é obtida girando a curva z = x 2 , 0 ≤ x ≤ 4 , em torno do eixo z , pede-seb) A área da porção de S compreendida entre os cilindros x 2 + y 2 = 1 e x 2 + y 2 = 4 .