Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.1 - Ex. 51
Seja para todo x em (-1,1) e seja
Então para todo x em (-1,1) e , onde quer que exista em (-1,1). Mas, para x em (-1,1). Porque o Teorema que diz que se duas funções diferentes derivadas são iguais para o mesmo intervalo está errado? (Teorema 5.1.2 do Livro de cálculo 1 do LEITHOLD, 3ed.)
Passo 1
A gente se depara de cara com uma questão de “prove”, mas relaxem galera, vamos com calma. De cara, encaramos com duas funções. . Primeiro, vamos esboçar elas.
fica:
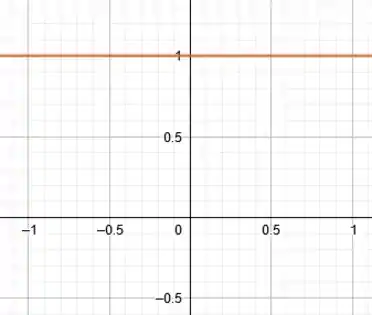
fica:
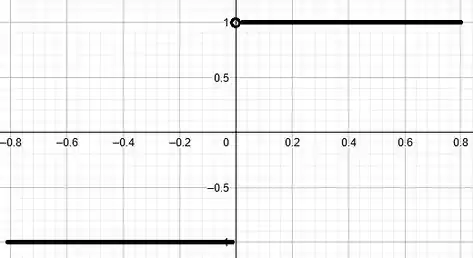
Passo 2
Aqui não tem segredo, a questão nos apresenta somente o porque das duas funções terem o mesmo intervalo (constantes) e nos fala que a derivada de uma constante é 0. E ela nos pergunta porque as derivadas são diferentes (já que as duas são supostamente feitas somente por constantes e a derivada de uma constante é 0). Ora mais, isso é fácil galera! Não observou? A função é derivável e igual a 0, porque é contínua. Mas a função não é continua, portanto não é derivável no intervalo dado!!
Resposta
Ei, a resposta está no passo a passo :)