Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.4 - Ex. 8

Seja B o triângulo de vértices 0,0 , 1,0   e 1,1 ; γ a fronteira de B orientada no sentido anti-horário. Verifique que

∫ γ P d x + Q d y = ∬ B ∂ Q ∂ x - ∂ P ∂ y d x   d y

Onde P e Q são supostas de classe C 1 num aberto Ω contendo B .

(Sugestão: Calcule ∬ B ∂ Q ∂ x d x d y fixando, inicialmente, y ; calcule - ∬ B ∂ P ∂ y d x d y fixando, inicialmente x . Compare, em seguida, com as integrais ∫ γ Q d y e ∫ γ P d x .

Passo 1

A curva em questão é dada pela imagem a baixo que criamos no software Geogebra

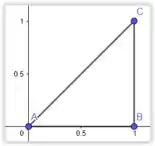
O Sentido que devemos adotar é o anti-horário, ou seja, A → B → C → A

Passo 2

Seguindo a sugestão, vamos primeiro verificar as integrais ∬ B ∂ Q ∂ x d x d y e ∬ B ∂ P ∂ y d x d y

Assim vamos fazer

∬ B ∂ Q ∂ x d x d y = ∫ 0 1 ∫ y 1 ∂ Q ∂ x d x d y

Onde pelo teorema fundamental do Cálculo, temos que

∫ 0 1 ∫ y 1 ∂ Q ∂ x d x d y = ∫ 0 1 Q x , y y 1 d y = ∫ 0 1 Q 1 , y - Q y , y d y

Segue o mesmo para P , ficando com

∬ B ∂ P ∂ y d x d y = ∫ 0 1 ∫ 0 x ∂ P ∂ y d y d x = ∫ 0 1 P x , x - P x , 0 d y

Passo 3

O que queremos fazer agora é calcular com a integrais de linhas. Assim fazemos

∫ γ Q d y = ∫ γ 1 Q d y + ∫ γ 2 Q d y + ∫ γ 3 Q d y

Que dada a parametrização γ 1 t = t , 0 , γ 2 t = 1 , t e γ 3 t = 1 - t , 1 - t

Já vemos que para γ 1 , temos que a integral é nula, visto que d y = 0

Ai teremos então

∫ γ Q   d y = ∫ 0 1 Q 1 , t d t + ∫ 0 1 Q 1 - t , 1 - t d t

Agora fazemos o seguinte, a primeira integral, tome t = y (trocando uma váriavél por outra não muda a integral) e para a segunda integral, fazemos t = x → 1 - x = y , nossa reta, assim temos

∫ γ Q d y = ∫ 0 1 Q 1 , y d y - ∫ 0 1 Q y , y d y = ∫ 0 1 Q 1 , y - Q y , y d y

E para P ( x , y )

∫ γ P d x = ∫ γ 1 P d x + ∫ γ 2 P d x + ∫ γ 3 P d x

Olhando pra nossa parametrização, aqui teremos que γ 2 é nossa integral nula, visto que d x = 0

Assim teremos

∫ γ P d x = ∫ 0 1 P t , 0 d t + ∫ 0 1 P 1 - t , 1 - t d t

Seguindo a mesma lógica do anterior, teremos

∫ γ P d x = ∫ 0 1 P x , 0 d x - ∫ 0 1 P x , x d x

Que colocando tudo em uma única integral, ficamos com

∫ γ P d x =   - ∫ 0 1 P x , x - P x , 0 d x

Passo 4

Assim temos que

∫ γ P d x + Q d y = ∫ 0 1 Q 1 , y - Q y , y d y - ∫ 0 1 P x , x - P x , 0 d x  

E

∬ B ∂ Q ∂ x - ∂ P ∂ y d x   d y = ∫ 0 1 Q 1 , y - Q y , y d y - ∫ 0 1 P x , x - P x , 0 d x  

Assim temos que

∫ γ P d x + Q d y = ∬ B ∂ Q ∂ x - ∂ P ∂ y d x   d y

Como queríamos mostrar

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12. Calcular a área da elipse x = 6 c o s θ ,y = 2 s e n θ .
8. ∮ C f → ⋅ d r → , onde f → = ( x 2 + 4 x y , 2 x 2 + 2 x + y 2 ) e C é a elipse x 2 + 4 y 2 = 16 , no sentido anti-horário
Nos exercícios 1 a 11, calcular as integrais curvilíneas dadas usand o teorema de Green.4. ∮ C - 2 x 2 y d x + 8 - ln ⁡ y + 2 d y , ao longo do paralelogramo de vértices (0,0), (2,0), (3,2) e (0,2), n
7. ∮ C f → ⋅ d r → , onde f → = ( y , 0 ) e C é o triângulo de vértices A(0,1), B(3,1) e C(2,2), no sentido horário.
16. Dado o campo vetorial f → = y x 2 + y 2 , - x x 2 + y 2 , mostrar que ∮ C f → ⋅ d r → = - 2 π para toda curva fechada simples C, suave por partes, orientada no sentido anti-horário que circunda a