Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.4 - Ex. 8
Seja e use um recurso gráfico para conjecturar o valor de . Depois tome e use o recurso gráfico e sua operação de traçar retas para encontrar um número positivo , tal que se .
Passo 1
Então pessoal, se plotarmos o gráfico de teremos:
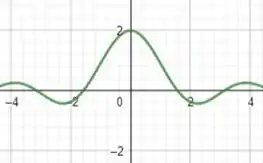
Observando o gráfico, podemos facilmente saber qual é o limite para quando , não é? É esse aqui ó:
Passo 2
Ainda do gráfico conseguimos retirar os seguintes pontos, pessoal:
Como temos dois valores de e dois valores de , podemos definir e . Ademais, temos que:
Logo:
Sendo assim, podemos tomar um delta mínimo, tal que:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 4 )g s = { s + 3 ,s es ≤ - 2 3 - s ,s e - 2s a ) lim s → - 2 + g s ;
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 7 )g r = { 2 r + 3 ,s er1 2 ,s er = 1 7 - 2 r ,s e1r a ) lim r → 1 +
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 6 )h x = {2 x + 1 ,s ex3 10 - x ,s e3 ≤ x a ) lim x → 3 + h x ; b ) l
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 1 )f x = { 2 ,s ex1 - 1 ,s ex = 1 - 3 ,s e1x a ) lim x → 1 + f x ; b
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 3 )f t = { t + 4 ,s et ≤ - 4 4 - t ,s e - 4t a ) lim t → - 4 + f t ;