32) Sejam f x = x - 1 2 , g x = e - 2 x e h x = 1 + ln ⁡ 1 - 2 x .(a) Determine as linearizações para f , g e h em a = 0 . O que você observa? Como explicar o que aconteceu?(b) Faça os gráficos de f , g e h e de suas aproximações lineares. Para qual função a aproximação é melhor? Para qual é pior? Justifique.

A linearização para as três funções em a = 0 é a mesma. Isso ocorre, pois quando x = 0 as três funções tem a mesma inclinação, ou seja, a mesma reta tangente: L x = 1 - 2 x .Melhor para h x e pior para f ( x ) .

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.10 - Ex. 32

32) Sejam , e .

(a) Determine as linearizações para , e em . O que você observa? Como explicar o que aconteceu?

(b) Faça os gráficos de , e e de suas aproximações lineares. Para qual função a aproximação é melhor? Para qual é pior? Justifique.

Passo 1

Nessa questão queremos obter a linearização das funções a seguir em .

E para isso vamos usar a seguinte fórmula:

Ou seja, vamos precisar derivar essas funções.

Por fim, no item b) devemos graficar as funções e suas aproximações e ver o que acontece.

Passo 2

Para obter a linearização uma função , devemos utilizar a aproximação da função em :

As funções são:

Vamos obter as suas derivadas:

Passo 3

Agora, vamos obter as linearizações das funções em por meio da fórmula:

Para :

Podemos ver que a linearização para as três funções em é a mesma. Isso ocorre, pois quando as três funções tem a mesma inclinação, ou seja, a mesma reta tangente.

Passo 4

Agora para o item b) vamos obter o gráfico.

Plotando as funções no gráfico temos:

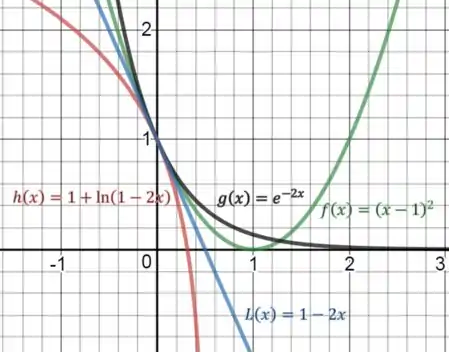
Pelo gráfico, vemos que a linearização se aproxima melhor da função do que para as demais, isso ocorre por que as demais mudam drasticamente o comportamento depois de .

A pior linearização é para a

Resposta

A linearização para as três funções em é a mesma. Isso ocorre, pois quando as três funções tem a mesma inclinação, ou seja, a mesma reta tangente: .Melhor para e pior para .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No exemplo 1, o peru é removido do forno quando sua temperatura atinge 185° F e colocado sobre uma mesa em uma sala onde a temperatura é de 75° F. Após dez minutos a temperatura é de 172° F, e após 20

O gráfico indica como a população da Austrália está envelhecendo, apontando o passado e a porcentagem projetada da população com idade superior ou igual a 65 anos. Use uma aproximação linear para prev

Verifique a aproximação linear dada em a = 0 . Então determine os valores de x para os quais a aproximação linear é precisa dentro de 0,1. 1 - x 3 ≈ 1 - 1 3 x

Use o método de Newton com a aproximação inicial especificada x 1 para encontrar x 3 , a terceira aproximação para a raiz da equação dada. (Responda com quatro casas decimais). 2 x 3 - 3 x 2 + 2 = 0 ;

Linearize a função:f (x) = x^3 - x^2 + 3 , a = - 2