Sejam e , onde e são as funções cujos gráficos estão representando a seguir.
a) Encontre
b) Enontre
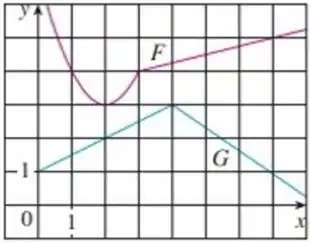
Passo 1
Fala aí, tudo certinho com você?
Bom essa questão definiu pra gente duas funções, sendo elas
e
Onde e estão no gráfico abaixo representadas no:
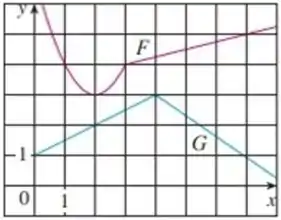
O que teremos que encontrar são os valores de e de e para isso precisaremos das informações do gráfico e das regras apropriada de derivação.
Para encontrar a partir da relação
Podemos usar a regra do produto, já que ela é formada por uma multiplicação entre duas funções.
Já para encontrar a partir de
Usaremos a regra do quociente.
Bom, vamos ver tudo isso acontecendo no passo a passo abaixo. Vem que te ajudo em cada detalhe.
Passo 2
a)
Para acharmos o valor de precisamos primeiro derivar a função . Para isso usaremos a Regra da Derivada do Produto, assim:
Logo, temos que
Para achar esses valores, devemos olhar para o gráfico.
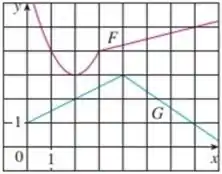
Dali, temos que e .
Já os valores de
e
medem cada um a inclinação da reta tangente às suas respectivas curvas, no ponto .
Assim, pelo gráfico, temos que
pois, a tangente é horizontal neste ponto
pois é a inclinação da reta que liga o ponto A ao ponto B.
Aplicando todas as informações na regra do produto, ficamos com:
Passo 3
b)
Para acharmos o valor de precisamos primeiro derivar a função . Para isso, usaremos a Regra da Derivada do Quociente, assim:
Logo, temos
Pelo gráfico, poderemos obter esses valores :
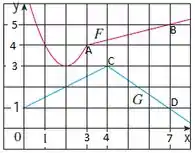
Assim, temos que
inclinação da reta que liga os pontos A e B)
inclinação da reta que liga os pontos C e D).
Substituindo todas as informações na regra do quociente, teremos:
O que nos dá:
E prontinho.