7. Sejam e funções com derivadas parciais continuas no plano xy tais que

Em R² exceto nos pontos . Indique por as circunferenciais de equações

Respectivamente, orientadas no sentido anti – horário. Sabendo que

Calcule

Neste capítulo trabalhamos conceitos de funções vetoriais, Teorema de Green e Campo conservativo. Vamos ter que lançar mãos de tudo isso para resolver nossas questões. Bora fazer uma revisão de leve nos teoremas. O Teorema de Green diz

Outra forma de enxergar seria

Quando nosso campo é conservativo, acontece que

Podemos fazer o rotacional e descobrir isso, ou por uma simples propriedade de diferenciação saber que

e quando o nosso campo é conservativo podemos dizer que existe uma função Potencial U, de forma que

Beleza? É bom fazer essa revisãozinha pra a gente já chegar afiado nas questões!!!!

Outra forma de enxergar esse teorema é dizer que

O trabalho ao percorrer a borda é igual ao fluxo que atravessa dentro da região limitada por essa borda. Então quando dizemos

Queremos dizer que não há fluxo que atravessa a região. O diferencial dessa questão é que ela põe exceções – “exceto nos pontos ”. Isso quer dizer que existe fluxo atravessando por esses 3 pontos. Então temos que observar a geometria do nosso sistema

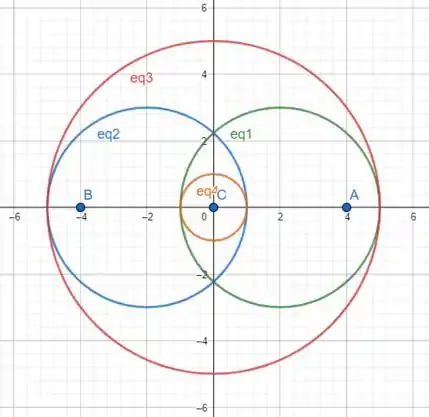
O pontos em azul são nossas excessoes. E os círculos são

Verde

Azul

Vermelho

Laranja

O circulo vermelho é nossa totalidade então dentro dele há o somatório de todos os fluxos

Outra forma de escrever isso é

Agora já o circulo verde cerca apenas A e C

Agora o circulo azul cerca os pontos A e B

Lembrando que queremos saber o fluxo do circulo laranja, logo queremos saber o fluxo de C. Podemos fazer um sisteminha

Com isso podemos dizer que

Logo nossa integral

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )