Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.2 - Ex. 45
Sejam polinômios, e suponha . Discuta o comportamento do gráfico de na vizinhança do ponto . Dê exemplos que apoiem suas conclusões.
Passo 1
Fala aí, tudo joia?
Olha só, a situação é a seguinte: temos dois polinômios, sendo que . A gente quer saber como vai ser o gráfico da função que divide um pelo outro, nesse ponto onde o polinômio debaixo zera.
Mas o denominador não pode zerar!! O que será que vai acontecer ali na vizinhança desse ponto então?
Passo 2
Olha só, o que vai acontecer é que o gráfico não vai passar no ponto . Vai passar muito, muito perto, mas não vai chegar nele.
Assim, na vizinhança desse ponto a função vai tender a infinito (negativo ou positivo). Quer dar uma olhada nuns exemplos?
Veja o caso de e . A gente tem que . Então vamos ver o comportamento do gráfico de nas vizinhanças de :
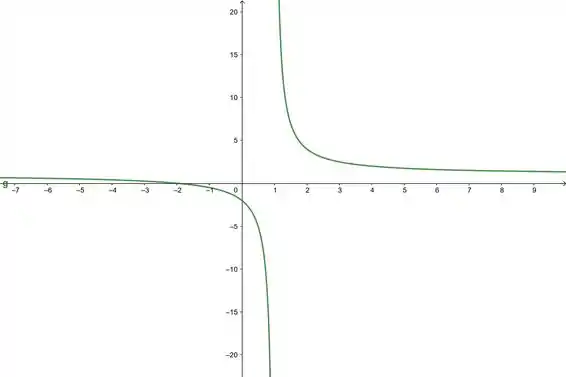
Viu? Os valores vindo pela esquerda tenderam ao infinito negativo, e as vindo pela direita ao infinito positivo.
Passo 3
Outro exemplo, agora com função quadrática:
Sabemos que , então vemos ver o comportamento de
perto de :
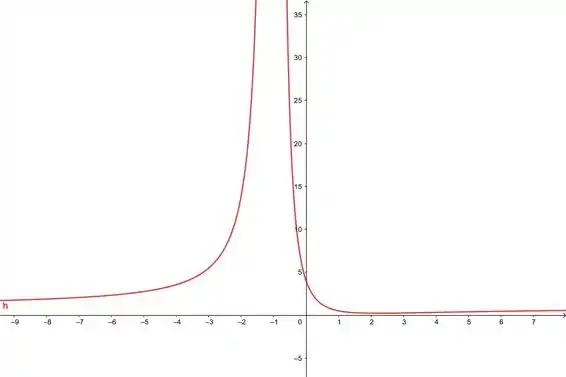
Aqui de ambos os lados a função tendeu a infinito. Vai ser sempre de uma dessas formas😉
Resposta
Ei, a resposta está no passo a passo :)