Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 2.Exercícios - Ex. 21
Seja
- verifique gráfica e analiticamente que f(x) possui um zero no intervalo [0,1];
- justifique teoricamente o comportamento da seqüência {xk} colocada a seguir, gerada pelo método de Newton para o cálculo do zero de f(x) em (O, 1), com Xo = 0.9 e precisão E = 5 x lo--6.
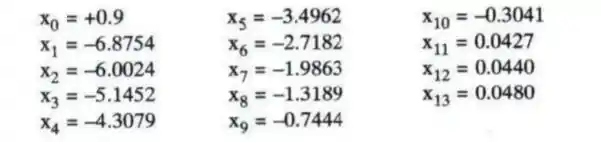
Passo 1
Vamos começar pela letra a:
Então ,sabemos que essa função é contínua nesse intervalo
Agora é só checar os sinais nos extremos do intervalo!
Então a gente sabe que tem um zero ali!
Passo 2
Vamos dar uma olhada no gráfico:
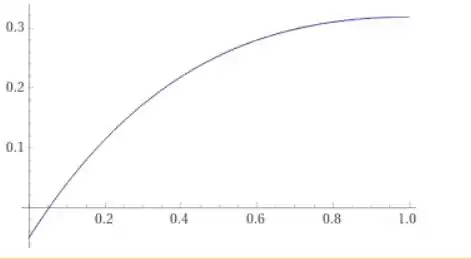
Agora com um sabemos que no ele fica travado naquele valor né, mas por que?
Se olharmos para o gráfico da derivada de , podemos ver que :
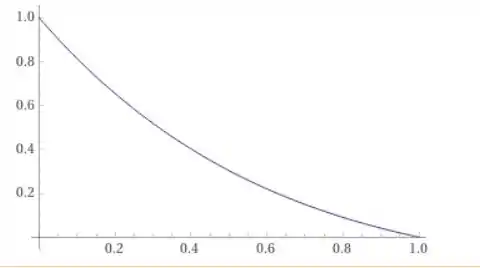
Ou seja, o valor do está muito próximo da raiz da derivada de , e sabemos que isso dá ruim no método de Newton!
Resposta
Olhar resolução
Exercícios de Livros Relacionados
Seja f x = x 4 - x 3 . Mostre que a equação f x = 75 tem uma solução no intervalo [3,4] e use o métdo de Newton para determiná-la.
Seja f x = 3 x - x 3 . Mostre que a equação f x = - 4 tem uma solução no intervalo [2,3] e use o método de Newton para determiná-la.
Deduza o método de Newton a partir de sua interpretação geométrica.
Aplique o método de Newton-Raphson à equação: x 3 - 2 x 2 - 3 x + 10 = 0 com x 0 = 1.9 . Justifique o que acontece.
Encontre uma raiz da equação: p ( x ) = x 4 - 6 x 3 + 10 x 2 - 6 x + 9 = 0 , aplicando o método de Newton para polinômios.