Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.4 - Ex. 1

Use o Teorema de Pitágoras para encontrar o comprimento do segmento de reta de y = 2 x entre 1,2 e   ( 2,4 ) e confirme que o valor está de acordo com o comprimento calculado usando:

  1. Fórmula (4)
  2. Fórmula (5)

Passo 1

Vamos calcular por Pitágoras primeiro. Dá uma olhada na figura:

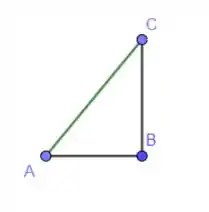
Sendo que A C aqui é nossa função f x = 2 x no intervalo entre os pontos.

Aplicando Pitágoras, a gente tem:

A C 2 = A B 2 + C B 2  

A C 2 = 1 2 + 2 2

A C 2 = 5

A C = 5

Prontinho! O comprimento de 2 x no intervalo pedido então é 5 .

Passo 2

  1. Vamos verificar agora se o valor confere com o que a gente acha usando a fórmula 4 . Pra essa a gente tem que fazer:

    2. d y d x = 2

    E aplicamos:

    ∫ 1 2 1 + 2 2   d x

    = ∫ 1 2 5   d x

    = 5 2 - 5  

    = 5

    Aqui conferiu!

    Passo 3

  2. Pra usar a fórmula 5, a gente tem que colocar tudo em função de y :

y = 2 x → x = y 2

Aí a gente deriva:

d x d y = 1 2

E aplicamos nos intervalos de y agora:

∫ 2 4 1 + 1 2 2 d y

∫ 2 4 1 + 1 4 d y

∫ 2 4 5 4   d y

= 5 2 4 - 5 2 2

= 2 5 - 2

= 5

E conferiu também!

Resposta

L = 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Passe a curva dada para coordenadas polares e desenhe-a:x4 – y4 = 2xy
Desenhe a curva a seguir utilizando coordenadas polares ρ ² = t g ( 2 θ ) ² , 0 ≤θπ 4( p ≥ 0 )
Passe a curva para coordenadas polares e desenhe-a: x² + y² + x = ( x ² + y ² ) ² ²
Calcule a área da região dada (coordenadas polares): ρ = cos ⁡ 2 θ
3. Calcule a área limitada pela curva (coordenadas polares).d) ρ = cos ⁡ 3 θ