Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.5 - Ex. 72
Simplifique a expressão.
Passo 1
Fala aí meu povo! Agora o negócio ficou um pouquinho mais difícil! E agora? Seno de arco cosseno? Que que isso?
Calma! Você já viu um monte de questões com as funções trigonométricas inversas (arco cosseno, arco seno, arco tangente e etc...). Mas vamos lembrar! A função arco cosseno é a inversa do cosseno.
Se:
Então:
Viu? É só a gente ir devagar que tudo se esclarece!
Aqui queremos simplificar a expressão:
Então eu já vou te adiantar que, pra organizar os nossos dados e equação, a gente vai fazer uma substituição. Vamos pegar esse arco cosseno que está dentro do seno e chamar de :
Hmmm, já ficou mais bonitinho ne?
Então fazendo a substituição na expressão que queremos calcular, o que temos que achar vai ficar:
Então vamos pro passo 2!
Passo 2
Bem, se definimos que
Então invertendo (ou aplicando a função cosseno dos dois lados da equação), vamos ficar com:
Veja o triangulo que representa esta relação:
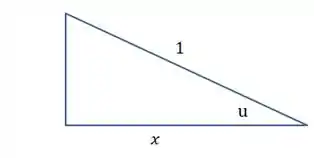
O lado que ainda não temos pode ser obtido do teorema de Pitágoras. Ou então, se a gente não quiser trabalhar com geometria, podemos retirar da relação fundamental da trigonometria:
Então:
Relembrando que :
E o triângulo fica:
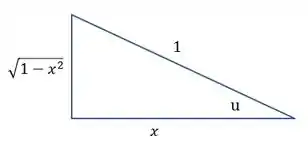
Passo 3
Bem, nós achamos que:
Mas se lembra o que a gente tava procurando pra começar a questão. Nós queremos calcular:
E pra isso temos a relação perfeita: A FÓRMULA DO ARCO DUPLO!
Pelo triângulo, nós já vimos que
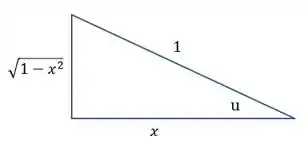
Então basta substituir na relação acima:
E nossa resposta é: