Enunciado

Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 4.Exercícios - Ex. 71

Qual é o sinal de cada uma das seguintes expressões?

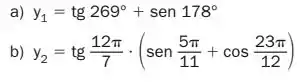
Passo 1

Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!

Para resolver este exercício vamos levar em consideração os sinais das funções trigonométricas em determinado quadrante.

Logo, vamos deixar algumas coisas claras:

Função Seno: positiva no primeiro e segundo quadrante.

Função Cosseno: positiva no primeiro e quarto quadrante.

Função tangente: positiva no primeiro e terceiro quadrante.

Passo 2

Com tudo isso exposto vamos a resolução.

Item a)

Temos a função tangente no terceiro quadrante, ou seja, um termo positivo, somando com seno no segundo quadrante, um termo também positivo.

Sabemos, que a soma de dois termos positivos, dá um termo positivo, então:

Item b)

Temos a função tangente no quarto quadrante, um termo negativo, multiplicando a soma de um seno no primeiro quadrante com um cosseno no quarto quadrante.

Sabemos que a soma de um seno no primeiro quadrante com um cosseno no quarto quadrante será positiva, pois os dois termos são positivos. E multiplicando esse valor por uma tangente no quarto quadrante (negativa) teremos uma expressão negativa.

Logo:

Resposta

Exercícios de Livros Relacionados

Sabendo que c o t gπ 4 = 1 e c o t g3 π 4 = - 1 e verificando que π 4 e7 π 4 são simétricos em relação ao eixo u, assim como 3 π 4 e 5 π 4 , dê o valor de c o t g7 π 4ec o t g5 π 4 .

Usando a simetria e sabendo que c o t gπ 6 = 3 , dê o valor da cotangente de 5 π 6 , 7 π 6e11 π 6 .

Qual é o sinal de cada uma das seguintes expressões?

Qual é o sinal das seguintes expressões:

Dado que c o s x = (2)/(5) e (3 pi)/(2)x2 pi , calcule o valor da expressãoy = (1 + t g^2 x)^2 + (1 - t g^2)^2