Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 4.Exercícios - Ex. 84
Qual é o sinal das seguintes expressões?
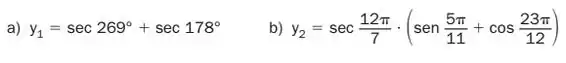
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Para isso, vamos expor algumas coisas aqui:
A função secante é positiva no primeiro e no quarto quadrante, e negativa nos demais. A função cosseno segue a mesma regra.
Já para a função seno temos que esta é positiva no primeiro e no segundo quadrante e negativa nos demais.
Passo 2
Com tudo isso exposto acima, podemos prosseguir com a resolução do exercício:
Item a)
Temos a soma de duas secantes, e os seus arcos se encontram no segundo e no terceiro quadrante, e nesses quadrantes a função secante é negativa, e sabemos que a soma de dois termos negativos resulta em um termo negativo.
Assim:
Item b)
Já neste item temos um produto de trigonométricas, então vamos analisar os dois sinais e usar a regra de sinais para definir o sinal de .
Temos uma secante no quarto quadrante (positiva) multiplicando a soma de um seno no primeiro quadrante (positivo) e um cosseno no quarto quadrante (também positivo).
Desse modo, o sinal resultante será positivo.