Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.3 - Ex. 48

∑ n = 1 ∞ 1 n 4   c o n v e r g e  

  1. s 30 = ∑ n = 1 30 1 n 4 é utilizado para estimar o valor de ∑ n = 1 ∞ 1 n 4 .

  2. Encontre n de forma que a soma parcial s n = ∑ i = 1 n 1 i 4 estime o valor de ∑ n = 1 ∞ 1 n 4 com um erro máximo de 0,000001.

Passo 1

Eae gente tudo certo?! Bora resolver uma questãozinha de método integral, dessa vez olhando o erro.

  1. Sabemos da teoria que o erro dado pela soma parcial para estimar uma somatória começa em n+1:

    2. ∑ n = 3 1 ∞ 1 n 4

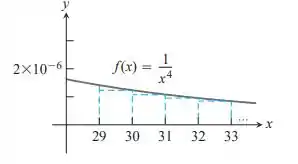
    Essa é a estimativa da área debaixo da curva f ( x ) = 1 / x 4 quando x for maior ou igual a 30, o comprimento dos retângulos no eixo x forem de 1 unidade e se o ponto final direito de cada subintervalo for considerado.

    Passo 2

    Portanto, vamos ver o limite da nossa integral para descobrir quanto é o erro,

    ∑ n = 31 ∞ 1 n 4 < ∫ 30 ∞ 1 x 4 d x = lim b → ∞ ⁡ ∫ 30 b 1 x 4 d x = lim b → ∞ ⁡ - 1 3 x 3 30 b

    = lim b → ∞ ⁡ - 1 3 b 3 + 1 3 30 3 = 1,23 ⋅ 10 ^ 5

    Dessa forma, o erro é < 1,23 ⋅ 10 5 .

    Passo 3

  2. Vamos direto ao ponto, só resolver uma inequação.

∫ n ∞ 1 x 4 d x < 0,000001

lim b → ∞ ⁡ ∫ n b 1 x 4 d x < 0,000001

lim b → ∞ ⁡ - 1 3 b 3 + 1 3 n 3 < 0,000001

1 3 n 3 < 0.000001

n > 69,33

n ≥ 70

Resposta

  1. o erro é < 1,23 ⋅ 10 5 .
  2. n ≥ 70 .

Exercícios de Livros Relacionados

Quais das séries nos Exercícios 17-54 convergem? E quais divergem? Utilize qualquer método e justifique suas respostas. ∑ n = 1 ∞ 1 n
Prove (a) a parte 2 e (b) a parte 3 do teste de comparação no limite.
Quais das séries nos Exercícios 17-54 convergem? E quais divergem? Utilize qualquer método e justifique suas respostas. ∑ n = 1 ∞ 1 1 + 2 + 3 + … + n
Quais das séries nos Exercícios 17-54 convergem? E quais divergem? Utilize qualquer método e justifique suas respostas. ∑ n = 1 ∞ t g hn n 2
Nos Exercícios 17-44, utilize qualquer método para determinar se a série converge ou diverge. Justifique suas respostas. ∑ n = 1 ∞ ln ⁡ n n