Substâncias dissolvidas em um aquífero são transportadas por dois mecanismos separados. O processo pelo qual um soluto é transportado pelo grande movimento do fluxo da água subterrânea é chamado de advecção. Além disso, o soluto é espalhado pelas flutuações em escala pequena na velocidade da água subterrânea ao longo de caminhos tortuosos do fluxo dentro de poros individuais, um processo chamado de dispersão mecânica. A forma unidimensional da equação de advecção-dispersão para uma substância dissolvida não reativa em um meio poroso isotrópico homogêneo saturado sob um fluxo uniforme regular é
![]()
em que c(x, t) é a concentração do soluto, υ é a velocidade linear média da água subterrânea, D é o coeficiente da dispersão hidrodinâmica e L é o comprimento do aquífero. Suponha que as condições de contorno são
![]()
e que a condição inicial é
![]()
em que f(x) é a concentração inicial dada do soluto.
Suponha que c(x, t) = X(x)T(t), use o método de separação de variáveis e encontre as equações satisfeitas por X(x) e T(t), respectivamente. Mostre que o problema para X(x) pode ser escrito na forma de Sturm-Liouville em que p(x) = r(x) = exp(–υx/D). Logo, os autovalores são reais e as autofunções são ortogonais em relação à função peso r(x).
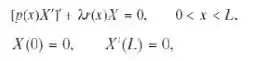
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos as deformações verticais de uma barra em suas condições de contorno. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser reescrever a equação diferencial.
Com isso, teremos o seguinte sistema de equações:
Lembrando a definição de Sturn-Liouville, temos:
Passo 3
Comparando as duas equações depois da aplicação da segunda derivada, obtemos:
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!