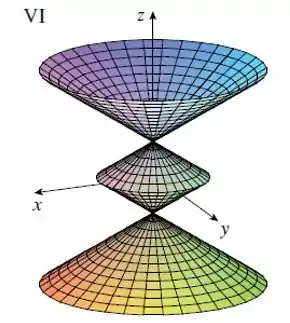
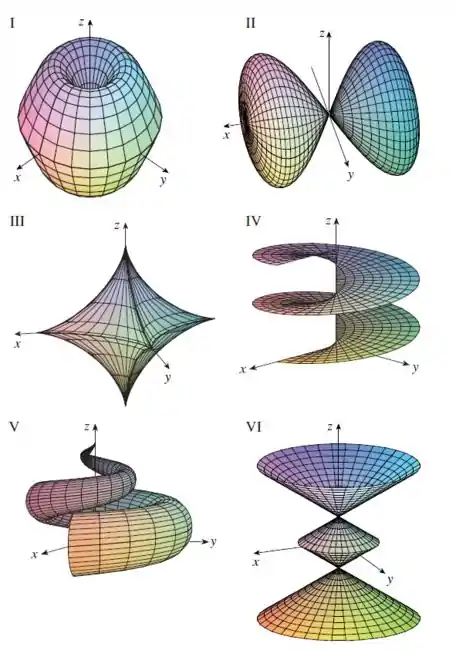
Faça uma correspondência entre as equações e os gráficos identificados por e justifique sua resposta. Determine quais famílias de curvas da grade têm constante e quais têm constante.
Passo 1
Faaaaala turminha, beleza!?
Nosso objetivo é fazer uma correspondência entre as imagens e a parametrização:
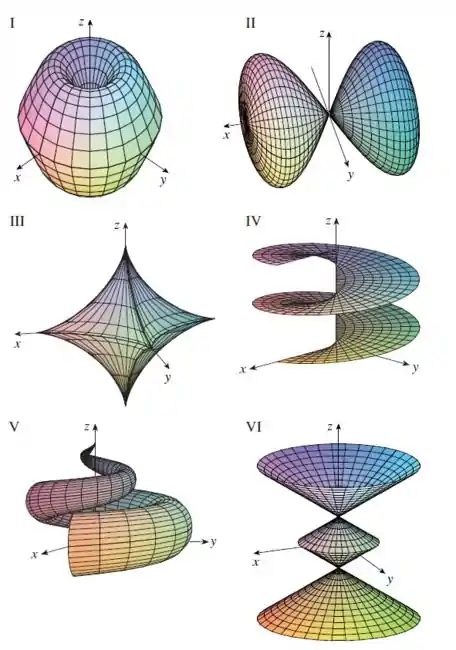
E também, determinar quais famílias de curvas da grade têm constante e quais têm constante.
Vamos começar avaliando a equação paramétrica. Temos que:
Tá, mas e agora?
Uma dica para você resolver é avaliar a família de curvas, faça . Assim, avalie a família de curvas que vai ser gerada.
Repare que no plano , temos uma parametrização típica de um círculo.
Sabendo disso, eu quero que você faça essa comparação. Aí você vai compreender que temos um círculo de raio no plano , como o raio pode variar e pode assumir qualquer valor de u, vamos gerar algo parecido com a figura no plano .
Vamos resolver essa!! Bora lá!
Passo 2
Vamos começar avaliando a família de curvas.
Para achar as famílias de curvas da grade correspondente a constante, vamos substituir:
Onde, é uma constante.
Substituindo nas parametrizações, vamos ter:
Olhando para essa parametrização e comparando com a de um círculo:
Assim, concluímos que temos um círculo no plano de raio igual a:
Logo, a podemos dizer que a parametrização representa a família de circunferências paralelas ao plano com raio:
E olhando os gráficos , vemos que eles possuem curvas de grade circular paralelas ao plano .
Porém só o gráfico tem curvas de grade circular com raio , vemos também que o raio é quando , além de que quando cresce o raio decresce, e se torna zero quando é , o que pode ser visto no gráfico .
Por fim, concluímos que o gráfico que representa a parametrização é a figura .
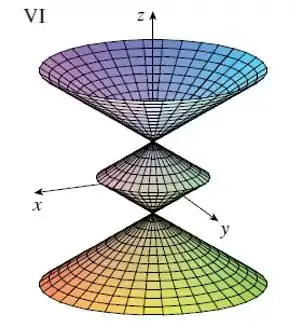
Resposta
Gráfico VI