Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.4 - Ex. 2
- Suponha e contínua em IR. Estude a função com relação a crescimento e decrescimento.
Passo 1
Para saber o crescimento e decrescimento de uma função, usamos a derivada.
Então, para a nossa questão, vamos estudar o intervalo da integral.
Passo 2
Aplicando em nossa questão:
Igualamos a zero para encontrar as raízes.
Passo 3
Resolvendo...
3x * ( x + 2 ) = 0
As raízes são -2 e 0
Graficamente:
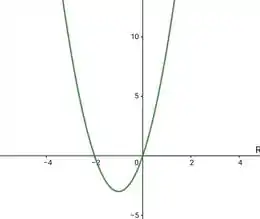
Sabemos que em uma função quadrática em que a concavidade é para cima, as partes de 'fora' serão positivas e a parte de 'dentro' será negativa.
Resposta
Exercícios de Livros Relacionados
Determine d y / d x se y = ∫ x 1 1 + t 2d t . Explique as principais etapas de seu cálculo.
Determine d y / d x : y = ∫ 2 x 2 + cos 3 td t
Determine d y / d x : y = ∫ 0 s e n - 1( x ) d t 1 - 2 t 2
Determine d y / d x : y = ∫ x 1 6 3 + t 4d t
Determine d y / d x : y = ∫ sec x 2 1 t 2 + 1d t