Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.3 - Ex. 3

Suponha que a função dada é estendida, periodicamente, para fora do intervalo original.

f x = L + x , - L ≤ x < 0 , L - x , 0 ≤ x < L

(a) Encontre a série de Fourier de função estendida.

(b) Esboce o gráfico da função para a qual a série converge por três períodos.

Passo 1

Vamos começar relembrando o que é a série de Fourier. A série de Fourier é uma função da forma:

f x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n π x L + b n sen ⁡ n π x L

Em que a 0 , a n e b n são constantes definidas para cada valor de n = 1 ,   2 ,   … ,   ∞ e, L corresponde ao intervalo original em que a função periódica é definida ( - L ≤ x < L ) . Usamos a série de Fourier como uma representação de uma função periódica g ( x ) qualquer, em que os valores de g ( x ) podem ser aproximados pela somatória de m termos da série f ( x ) . Agora que já relembramos o conceito da série de Fourier, vamos ao exercício.

Passo 2

O item (a) nos pede para encontrar a série de Fourier para a função periódica:

f x = L + x , - L ≤ x < 0 , L - x , 0 ≤ x < L

Como acabamos de relembrar, a série de Fourier é uma equação da forma:

f x = a 0 2 + ∑ n = 1 m a n cos ⁡ n π x L + b n sen ⁡ n π x L

Precisamos então obter os termos a 0 ,   a n ,   b n e L . O intervalo de uma função escrita como série de Fourier é definido como - L ≤ x < L . Então, para a nossa função L = L . Tudo bem?

O próximo passo é o cálculo dos coeficientes. O coeficiente a 0 é definido por:

a 0 = 1 L ∫ - L L f x d x

Substituindo a função f ( x ) :

a 0 = 1 L ∫ - L 0 ( L + x ) d x + ∫ 0 L ( L - x ) d x

a 0 = 1 L L x + x 2 2 - L 0 + L x - x 2 2 0 L

a 0 = 1 L 0 - L * - L + L 2 2 + L 2 - L 2 2 - 0

a 0 = 1 L L 2 2 + L 2 2 = 1 L L 2

a 0 = L

Agora vamos determinar a n . Ele é dado por:

a n = 1 L ∫ - L L f x cos ⁡ n π x L d x

Aplicando f ( x ) ficamos com

a n = 1 L ∫ - L 0 ( L + x ) cos ⁡ n π x L d x + ∫ 0 L ( L - x ) cos ⁡ n π x L d x

a n = 1 L ∫ - L 0 ( L ) cos ⁡ n π x L d x + ∫ 0 L ( L ) cos ⁡ n π x L d x + ∫ - L 0 ( x ) cos ⁡ n π x L d x - ∫ 0 L ( x ) cos ⁡ n π x L d x

a n = 1 L ∫ - L L ( L ) cos ⁡ n π x L d x + ∫ - L 0 ( x ) cos ⁡ n π x L d x - ∫ 0 L ( x ) cos ⁡ n π x L d x

a n = 1 L L 2 n π sen ⁡ n π x L - L L + L n π x sen ⁡ n π x L - L 0 - L n π ∫ - L 0 sen ⁡ n π x L d x - L n π x sen ⁡ n π x L 0 L - L n π ∫ 0 L sen ⁡ n π x L d x

a n = 1 L L 2 n π 2 cos ⁡ n π x L - L 0 - L 2 n π 2 cos ⁡ n π x L 0 L

a n = 1 L L 2 n π 2 cos ⁡ 0 - cos ⁡ - n π - L 2 n π 2 ( cos ⁡ n π - cos ⁡ 0 )

a n = a n = 1 L L 2 n π 2 1 - cos ⁡ n π + L 2 n π 2 1 - cos ⁡ n π

a n = 2 L n π 2 ( 1 - cos ⁡ n π )

Por fim, vamos calcular b n . Ele é dado por:

b n = 1 L ∫ - L L f x sen ⁡ n π x L d x

Substituindo f ( x ) :

b n = 1 L ∫ - L 0 ( L + x ) sen ⁡ n π x L d x + ∫ 0 L ( L - x ) sen ⁡ n π x L d x

b n = 1 L ∫ - L 0 ( L ) sen ⁡ n π x L d x + ∫ 0 L ( L ) sen ⁡ n π x L d x + ∫ - L 0 ( x ) sen ⁡ n π x L d x - ∫ 0 L ( x ) sen ⁡ n π x L d x

b n = 1 L ∫ - L L ( L ) sen ⁡ n π x L d x + ∫ - L 0 ( x ) sen ⁡ n π x L d x - ∫ 0 L ( x ) sen ⁡ n π x L d x

b n = 1 L - L 2 n π   cos ⁡ n π x L - L L - L n π x cos ⁡ n π x L - L 0 + L n π ∫ - L 0 cos ⁡ n π x L d x - - L n π x cos ⁡ n π x L 0 L + L n π ∫ 0 L cos ⁡ n π x L d x

b n = 1 L - L n π ( 0 - ( - L cos ⁡ n π ) - - L n π ( L cos ⁡ n π - 0 )

b n = 1 L - L 2 n π cos ⁡ n π + L 2 n π cos ⁡ n π

b n = 0

Aplicando na função:

f x = L 2 + ∑ n = 1 m 2 L n π 2 ( 1 - cos ⁡ n π ) cos ⁡ n π x L

O termo 1 - cos ⁡ n π terá valor 0 para n par e valor 2 para os n ímpar. Tudo bem? Se não ficou claro, vamos usar o exemplo de n = 1 e n = 2 . Para n = 1 :

cos ⁡ π = - 1 → 1 - cos ⁡ n π = 2

Para n = 2 :

cos ⁡ 2 π = 1 → 1 - cos ⁡ n π = 0

Então, para o somatório da parte cosseno apenas os valores de n ímpar são relevantes. Para garantir que vamos somar apenas os termos ímpares vamos substituir n por 2 n - 1 e, 1 - cos ⁡ n π por 2. Tudo bem?

Então

f x = L 2 + ∑ n = 1 m 2 L ( 2 n - 1 ) π 2 ( 2 ) cos ⁡ ( 2 n - 1 ) π x L

f x = L 2 + 4 L π 2 ∑ n = 1 m cos ⁡ 2 n - 1 π x / L 2 n - 1 2

Passo 3

Agora que temos a série de Fourier, vamos para o item (b). Ele nos pede para esboçar o gráfico da série para três períodos. Para isso, vamos assumir um valor arbitrário de L , L = π , e utilizar o Excel para obter os coeficientes a 0 ,   a n e b n e, para realizar o somatório. Aplicando a série para os intervalos - 3 π ≤ x < - π , - π ≤ x < π e π ≤ x < 3 π , devemos obter algo da forma:

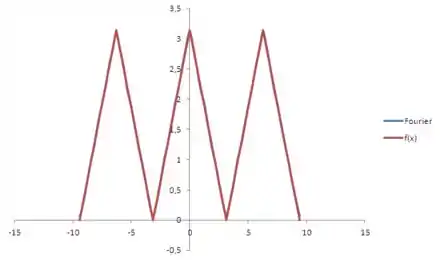
Esta foi a função obtida somando 10 termos da série. Podemos ver que a série já começa a se aproximar da função f ( x ) . Caso seja necessário uma aproximação mais fiel, deveríamos aumentar o número de termos do somatórios.

Resposta

(a) f x = L 2 + 4 L π 2 ∑ n = 1 m cos ⁡ 2 n - 1 π x / L 2 n - 1 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x , - π ≤ x0 , 0 , 0 ≤ xπ f x + 2 π = f ( x ) (a) Encontre a série de Fourier da função dada.(b) Seja e n
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x + 2 , - 2 ≤ x0 , 2 - 2 x , 0 ≤ x2 f x + 4 = f ( x ) (a) Encontre a série de Fourier da função dada.(b) S
Encontre a solução formal do problema de valor inicial y ' ' + ω 2 y = f ( t ) , y 0 = 0 , y ' 0 = 0 Em que f é periódica com período 2 π e f t = 1 , 0tπ , 0 , t = 0 , π , 2 π , - 1 , πt2 π
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x - x 3 , - 1 ≤ x1 f x + 2 = f ( x ) (a) Encontre a série de Fourier da função dada.(b) Seja e n x = f x -
(a) Se f e f ' forem seccionalmente contínuas em - L → xL e se f for periódica com período 2 L , mostre que n a n e n b n permanecerão limitadas quando n → ∞ .(b) Se f for contínua em - L ≤ x ≤ L e pe