Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.3 - Ex. 9
Suponha que . Prove que existem , α e tais que, para todo ,
.
Interprete graficamente.
Passo 1
Vamos dar uma olhada na definição precisa de limite, temos que:
se para todo número houver um número tal que
se então
Passo 2
Vamos supor que , e sendo , para todo tal que para todo :
Para e :
Graficamente temos:
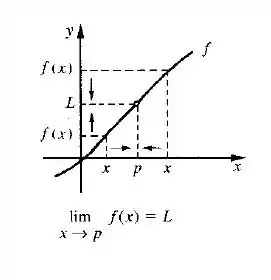
Aqui temos que está próximo de quando está próximo de , pois então nos diz que podemos fazer os valores de ficarem dentro de uma distância de de .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Ache d y d x por derivação implícita: cot - 1 x 2 3 y + x y 2 = 0
Ache a derivada da função G w = tan - 1 w - 3 3 w + 1 .
Expresse as quantidades dadas em termos do logaritmo natural. cosh - 1 2
Um holofote está a 1 2 km de uma estrada reta e mantém sua luz focalizada em um automóvel que está viajando a uma velocidade escalar constante de 60 km/h. Ache a taxa segundo a qual o feixe de luz est
Nos Exercícios 1-4:a. Determine f - 1 ( x ) .b. Esboce em um único gráfico f e f - 1 .c. Calcule d f d x em x = a e d f - 1 d x em x = f ( a ) para mostrar que nesses pontos d f - 1 d x = 1 d f d x .2