Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.5 - Ex. 23
Suponha que seja uma curva suave no intervalo e que para cada . Deduza uma fórmula para a área da superfície gerada quando a curva , , gira em torno da reta ().
Passo 1
O que acontece aqui é que em vez de girarmos uma curva totalmente positiva em torno do eixo , precisaremos girar em torno de uma reta paralela o eixo , localizada em , para formar nossa nova superfície.
E aí o que enunciado pede é para montarmos uma nova equação para conseguirmos calcular a área dessa nova superfície.
Vem comigo?
Passo 2
Primeiro vamos analisar os parâmetros que regiam a equação da área da antiga superfície, a que girava em torno de :
Olha na figura a curva que a gente tem, de uma forma genérica:
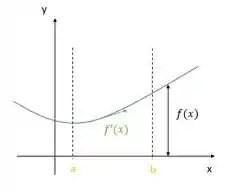
Vemos que é a inclinação da nossa curva, é o nosso intervalo e é a distância dos pontos da curva até o eixo de rotação.
Vamos seguir!
Passo 3
Vamos analisar a nova situação e ver como os nossos parâmetros mudaram.
Olha na figura a curva que a gente tem, de uma forma genérica:
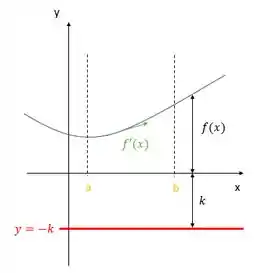
Vemos que e não mudam. Mas repara que distância dos pontos da curva até o eixo de rotação não é mais , e sim . E essa é a mudança que a gente vai fazer na equação antiga.
Se tínhamos isso:
No lugar de , colocamos :
Tá aí nossa equação novinha em folha! 😊