Suponha que a velocidade (em pés/s) de uma paraquedista segundos depois de saltar de um avião seja dada pela equação .
a) Faça o gráfico de versus .
b) Calculando um limite apropriado, mostre que o gráfico de versus tem uma assíntota horizontal com uma constante apropriada.
c) Qual é o significado físico da constante em b)?
Passo 1
a) Então galera, utilizando uma ferramenta gráfica para plotar o gráfico, teremos algo assim:
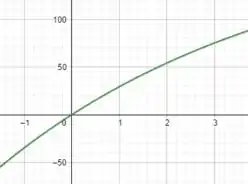
Passo 2
b) Para vermos se o gráfico possui assíntotas ou não, devemos calcular os limites no infinito da função, se liga:
Se aplicarmos o limite, teremos:
Ou seja, de fato possui uma assíntota horizontal no gráfico em.
Passo 3
c) Quando um corpo ou objeto está em queda livre há um momento em que a força peso e a força de arrasto se equilibram e fazem com que esse corpo pare de acelerar, isto é, em um certo instante de tempo o corpo começa a cair com uma velocidade constante , que é exatamente a velocidade encontrada na letra b). Essa velocidade recebe o nome de velocidade terminal.
Resposta
b)
c) Toda a explicação está no passo 3. O conceito físico associado se chama Velocidade Terminal.