Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.3 - Ex. 83b

83. b) Suponha que, em vez de serem iguais, os comprimentos ∆ x k dos subintervalos da partição de [ a ,   b ] variam em tamanho. Demonstre que:

U - L ≤ f b - f a ∆ x m a x ,

no qual ∆ x m a x é a norma de P , e que, portanto:

lim P → 0 ⁡ U - L = 0

Passo 1

Assim como fizemos na letra anterior, primeiramente devemos determinar quem são as somas superiores e quem são as somas inferiores, ok? As partições relacionadas ao máximo, que iremos chamar de U , será:

U = m a x 1 ∆ x 1 + m a x 2 ∆ x 2 + …   + m a x n ∆ x n

Mas po, quem são esses máximos aí? Esses máximos são os valores que a função apresenta no pontos de x , isto é:

m a x 1 = f x 1 ,   m a x 2 = f x 2 , …   , m a x n = f ( x n )  

Passo 2

Agora temos que determinar as partições relacionadas ao mínimo, certo? Esse mínimo chamaremos de L , ok? Fazendo a mesma coisa que fizemos no passo anterior, teremos:

L = m i n 1 ∆ x 1 + m i n 2 ∆ x 2 + …   + m i n n ∆ x n

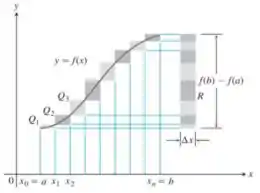
Mas quem são esses mínimos aí? De acordo com o gráfico, esses são os valores que a função apresenta nos pontos de x também, mas com uma diferença:

m i n 1 = f x 0 ,   m i n 2 = f x 1 , …   , m i n n = f ( x n - 1 )

Passo 3

Fazendo a diferença entre as somas superiores e inferiores, teremos que:

U - L = m a x 1 - m i n 1 ∆ x 1 + m a x 2 - m i n 2 ∆ x 2 ,   …   , m a x n - m i n n ∆ x n

U - L = f x 1 - f x 0 ∆ x 1 + f x 2 - f x 1 ∆ x 2 , …   , f x n - f x n - 1 ∆ x n

≤ f x 1 - f x 0 ∆ x m a x + f x 2 - f x 1 ∆ x m a x , …   , f x n - f x n - 1 ∆ x m a x

Simplificando essas contas feias, temos o seguinte:

U - L ≤ f x n - f x 0 ∆ x m a x

E como, de acordo com o gráfico, x n = b e x 0 = a , então:

U - L ≤ f b - f a ∆ x m a x

Assumindo agora a igualdade, teremos:

lim P → 0 ⁡ U - L = lim P → 0 ⁡ f b - f a ∆ x m a x

Desde que ∆ x m a x = P :

lim P → 0 ⁡ U - L = 0

CQD.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

21. Inscreva um polígono regular de n lados dentro de um círculo de raio 1 e calcule a área do polígono para os seguintes valores de n :a. 4 (quadrado)b. 8 (octógono)c. 16d. Compare as áreas obtidas n
20. Poluição do ar Uma fábrica gera energia elétrica pela queima de óleo. Os poluentes produzidos como resultado da combustão são removidos por purificadores colocados nas chaminés. Com o tempo, o mec
Nos Exercícios 15-18, utilize uma soma finita para estimar o valor médio de f no intervalo dado, dividindo-o em quatro subintervalos de comprimento igual e avaliando f nos pontos médios dos subinterva
22. ( Continuação do Exercício 21.)a. Inscreva um polígono regular de n lados dentro de um círculo de raio 1 e calcule a área de um dos n triângulos congruentes formados pelos raios que cruzam os vért
19. Poluição da água Há um vazamento de combustível em um petroleiro avariado no mar. A tabela a seguir mostra que a avaria apresenta uma piora, pois o vazamento aumenta a cada hora.a. Superestime e s