Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.8 - Ex. 5
A tabela dá estimativas da população mundial, em milhões, de a .
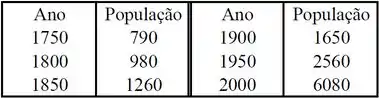
(a) Use o modelo exponencial e os valores da população para e para prever a população do mundo em e . Compare com os valores da tabela.
(b) Use o modelo exponencial e os valores da população para e para prever a população do mundo em . Compare com o valor da tabela.
(c) Use o modelo exponencial e os valores da população para e para prever a população do mundo em . Compare com o valor da tabela e tente explicar a discrepância.
Passo 1
Fala meus queridos, nessa questão nos é dado uma tabela com a população mundial em Milhões para 6 anos diferentes.
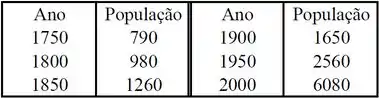
A partir desses dados, nos é pedido para estimar a população usando o modelo exponencial.
De acordo com esse modelo, podemos dizer que:
Dessa forma, podemos chamar de nossa função população com sendo o tempo em anos a partir do tempo inicial.
Usando as populações dadas na tabela podemos encontrar o parâmetro , e depois com esse parâmetro podemos usar o modelo para estimar as populações em outros anos.
Passo 2
Na letra a) queremos o seguinte:
(a) Use o modelo exponencial e os valores da população para e para prever a população do mundo em e . Compare com os valores da tabela.
Agora precisamos identificar as variáveis do problema. Sabemos que e que o valor de é desconhecido.
Sabemos que em , tomando este como o ano inicial a população, em milhões, era de , logo, (milhões) e após anos (que é o nosso ) a população é de (milhões) então (milhões). Aplicando esses valores na equação exponencial obtemos o seguinte:
Aplicando o logaritmo natural temos:
Como :
Logo, taxa de crescimento relativa corresponde a .
Tendo o valor de é só aplicar à equação exponencial para encontrar o , lembrando que anos:
(Milhões)
Para que é a população em 1950, o procedimento é mesmo, mas com , então:
1870,781338 (milhões)
Podemos ver que esses valores divergem dos valores reais;
Passo 3
Na letra b) o que queremos é:
(b) Use o modelo exponencial e os valores da população para e para prever a população do mundo em . Compare com o valor da tabela.
Neste item é usada a mesma ideia do item (a),só que agora usaremos o valor de início como os do ano de 1850 (milhões) e para calcular o utilizaremos o do ano 1900, onde , com isso, temos (milhões):
Para o ano de com :
2160,714286 (milhões)
Que é um valor mais próximo que o obtido anterior.
Passo 4
Por fim, na letra c) temos:
(c) Use o modelo exponencial e os valores da população para e para prever a população do mundo em . Compare com o valor da tabela e tente explicar a discrepância.
Neste item é usada a mesma ideia dos itens (a) e (b), só que agora usaremos o valor de início como (milhões) e para calcular o utilizaremos o (milhões) com o tempo anos:
Para com :
(Milhões)
O valor obtido é muito discrepante do real. Isso acontece por conta dos inúmeros fatores e fenômenos dos âmbitos sociais, políticos, religiosos, econômicos, dentre outros, que fazem com que a população mundial flutue fora da curva exponencial.
Resposta
(a) (milhões de pessoas) e 1870,781338 (milhões de pessoas)
(b) 2160,714286 (milhões de pessoas)
(c) (milhões de pessoas)