Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.1 - Ex. 7

A tabela mostra a posição de um ciclista

  1. Encontre a velocidade média nos períodos de tempo a seguir:
    1. [1,3]
    2. [2,3]
    3. [3,5]
    4. [3,4]
  2. Use o gráfico de s como uma função de t para estimar a velocidade instantânea quando t = 3 .

Passo 1

Eaeee, belezinha??? Bom... Temos um ciclista andando com sua biscicleta e o enunciado da uma tabelinha do tempo e do deslocamento dele:

E, na letra a, pede pra a gente encontrar a velocidade média em alguns períodos de tempo.

Pra isso a gente vai usar a seguinte fórmula:

v m e d = s t 2 - s t 1 t 2 - t 1

Os tempos são dados no enunciado e a gente só precisa pegar as posições na tabela!

Para a letra (b) a gente vai fazer um gráfico com os dados da tabela e vamos estimar a velocidade instantânea quando t = 3 , traçando uma reta tangente!

Bora lá!! 😉

Passo 2

Foca nessa fórmula que é ela que a gente vai usar:

v m e d = s t 2 - s t 1 t 2 - t 1

  1. Para [ 1,3 ]   a gente tem as posições [ 1,4 ; 10,7 ]

    2. v m e d = 10,7 - 1,4 3 - 1 = 9,3 2 = 4,65   m / s

  2. Para [2,3] as posições [ 5,1 ; 10,7 ]

    3. v m e d = 10,7 - 5,1 3 - 2 = 5,6 1 = 5,6   m / s

  3. Para [ 3,5 ] , as posições 10,7 ; 25,8

    4. v m e d = 25,8 - 10,7 5 - 3 = 15,1 2 = 7,55   m / s

  4. Para [3,4] as posições 10,7 ; 17,7

v m e d = 17,7 - 10,7 4 - 3 = 7 1 = 7   m / s

Passo 3

Agora a letra (b)!!!

Esboçando o gráfico, ficamos com:

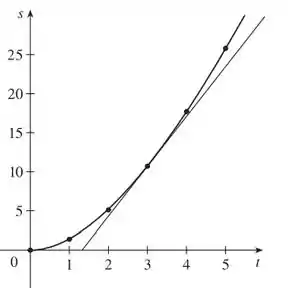
A velocidade instantânea é dada pela inclinação da reta tangente à curva no ponto t = 3 .

E o que a gente faz agora?!

A gente vai pegar dois pontos quaisquer dessa reta tangente para calcular sua inclinação!

Você pode fazer isso na mão mesmo, tomando bastante cuidado com a escala! Lembre-se, quanto melhor a escala mais preciso vai ser o resultado!!

Passo 4

Aqui eu vou usar os pontos ( 3 ; 10,7 ) e ( 1,3 ; 0 ) eu escolhi esses pontos, porque o primeiro é onde a reta tangente toca a curva, então esse ponto é preciso!

Já o segundo é quando a tangente intecepta o eixo x , esse valor é um pouco meno preciso mas já da pra a gente fazer uma estimativa!

Para estimar a v i n s t a n t a n e a fazemos:

v i n s t a n t a n e a = 10,7 - 0 3 - 1,3 ≈ 6,3   m / s

Você pode escolher outros pontos quaisquer, não tem problema!!

Resposta

    1. Para [1,3]

      2. v m e d = 4,65   m / s

    2. Para [2,3]

      3. v m e d = 5,6   m / s

    3. Para [3,5]

      4. v m e d = 7,55   m / s

    4. Para [3,4]

    v m e d = 7   m / s

  2. v i n s t a n t a n e a ≈ 6,3   m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule f ' x onde f x é igual a x 3 + x co s sec ⁡ x
Calcule f ' x onde f x é igual a cos ⁡ x + x 2 + 1 sen ⁡ x
Seja g x = x x 2 + 1 .Determine os pontos do gráfico de g em que as retas tangentes, nestes pontos, sejam paralelas ao eixo x .Estude o sinal de g ' x .Calcule lim x → + ∞ ⁡ g x e lim x → - ∞ ⁡ g x .U
Seja f x = x 3 + 3 x 2 + 1 .Estude o sinal de f ' x .Calcule lim x → + ∞ ⁡ f x e lim x → - ∞ ⁡ f x .Utilizando as informações acima, faça um esboço do gráfico de f .
Calcule f ' x . f x = 4 + 5 x 2 ln ⁡ x