Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 13
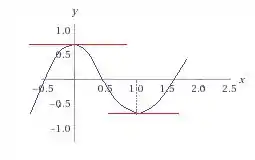
Dê exemplo (por meio de um gráfico) de uma função , definida e derivável em , tal que e .
Passo 1
Queremos as seguintes características no esboço do gráfico:
- Derivada nula para : ou seja, reta tangente horizontal para ;
- Derivada nula em : ou seja: reta tangente horizontal para ;
Passo 2
Para isso eu escolhi uma função polinomial de grau . Com a ajuda de um programa de geração gráfica, o esboço fica:
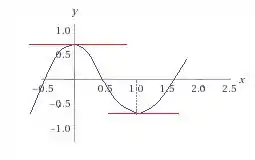
Passo 3
As retas em vermelho representam a derivada da função (em azul) em e em .
Resposta
Exercícios de Livros Relacionados
Um aluno que está estudando uma língua estrangeira tem 50 verbos para serem memorizados. A taxa segundo a qual o estudante pode memorizar esses verbos é proporcional ao número de verbos que restam a s
Determine d 999 d x 999 ( cos x )
Determine a fórmula para a derivada em relação a x de sec x c o s s e cx c o t gx
Coeficientes angulares no gráfico da função cotangente: Esboce em apenas um gráfico y = c o t g( x ) e sua derivada em 0xπ . O gráfico da função cotangente parece ter um coeficiente angular mínimo? E
Coeficientes angulares no gráfico da função tangente: Esboce em apenas um gráfico y = t g( x ) e sua derivada em ( - π / 2 ,π / 2 ) . O gráfico da função tangente parece ter um coeficiente angular mín