Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 1

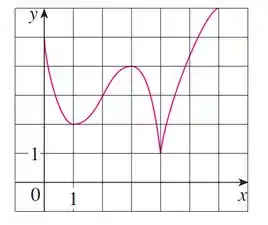
Usar o gráfico dado de f para encontrar o seguinte:

(a) Os intervalos abertos nos quais f é crescente.

(b) Os intervalos abertos nos quais f é decrescente.

(c) Os intervalos abertos nos quais f é côncava para cima.

(d) Os intervalos abertos nos quais f é côncava para baixo.

(e) As coordenadas dos pontos de inflexão.

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos o seguinte gráfico e vamos analisar o que se pede.

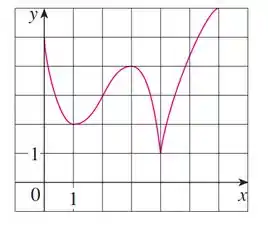
A função f é crescente em um intervalo se valores de x maiores correspondem a valores de f ( x ) maiores, ou seja, se ela cresce nesse intervalo.

f é decrescente em se valores de x maiores correspondem a valores de f x menores.

Já sobre a concavidade, ela é côncava para cima, se ela formar uma curva que faz um buraco para cima (um sorriso) e ela é côncava para baixo, se ela formar uma curva que faz um buraco para baixo (um rosto triste).

Já um ponto de inflexão é onde a função passa de uma concavidade para outra.

Passo 2

  1. f é crescente nos intervalos ( 1,3 ) e ( 4,6 ) .

  2. f é decrescente nos intervalos ( 0,1 ) e ( 3,4 ) .

    3. Passo 3

  3. f é côncava para cima (o “buraco” está voltado para cima, há um “formato de sorriso”) no intervalo ( 0,2 ) .

  4. f é côncava para baixo (o “buraco” está voltado para baixo, há um “formato de rosto triste”) no intervalo ( 2,4 ) e ( 4,6 ) .

    5. Passo 4

  5. O ponto de inflexão �� aquele onde a concavidade muda, que no caso, ocorre no ponto x = 2 , f x = 3 , logo é o ponto ( 2,3 ) .

Resposta

  1. ( 1,3 ) e ( 4,6 ) .
  2. ( 0,1 ) e ( 3,4 ) .
  3. ( 0,2 ) .
  4. ( 2,4 ) e ( 4,6 ) .
  5. ( 2,3 ) .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que lhe foi dada uma fórmula para uma função f .Como você determina onde f é crescente ou decrescente?Como você determina onde o gráfico de f é côncavo para cima ou para baixo?Como você locali
O gráfico da segunda derivada f ' ' de uma função f está mostrando. Diga as coordenadas x dos pontos de inflexão de f . Justifique sua resposta.
Usar o gráfico dado de f para encontrar o seguinte:(a) Os intervalos abertos nos quais f é crescente. (b) Os intervalos abertos nos quais f é decrescente. (c) Os intervalos abertos nos quais f é cônca
Suponha que todas as funções sejam duas vezes deriváveis e que as segundas derivadas nunca sejam nulas.Suponha que f e g sejam ambas côncavas para cima em - ∞ , ∞ . Sob que condições em f a função com
Mostre que as curvas y = e - x e y = - e - x tocam a curva y = e - x sen ⁡ x em seu ponto de inflexão.