Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 9

Dê exemplo (por meio de um gráfico) de uma função , definida e derivável em , tal que para todo .

Passo 1

Oi, galerinha! Nessa questão, a genre precisa achar uma função cuja derivada em deve ser menor do que em .

Para satisfazer essa condição, a gente pode pensar em uma função que tenha uma reta tangente decrescente para e positiva para .

A ideia é chutar uma função e ver se ela satisfaz essa condição!

Passo 2

Minha escolha vai ser uma parábola com boca pra cima que tem equação:

Com a ajuda de um gerador gráfico temos o esboço:

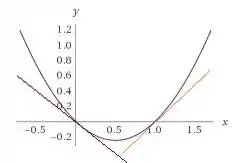
Repara que em vermelho temos a reta tangente a (curva azul) em . Essa reta é decrescente.

E em laranja temos a reta tangente a função em e ela é crescente. Então a derivada reresentada pela reta laranja é maior do que a derivada representada pela reta vermelha.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

48. Prove que o retângulo que tem a base no eixo x e dois vértices na curva y = e - x 2 , terá a maior área possível se os seus vértices estiverem nos pontos de inflexão do gráfico.

Dada f x = x 2 . Use uma calculadora para tabular valores de f 3 + ∆ x - f ( 3 ) ∆ x quando ∆ xé1 ,0,5 ,0,1 ,0,01 ,0,001 , e∆ xé - 1 ,- 0,5 ,- 0,1 ,- 0,01 ,- 0,001 é é . A que f 3 + ∆ x - f ( 3 ) ∆ x

40) Dada f x = x 3 . Use uma calculadora para tabular valores de f 2 + ∆ x - f ( 2 ) ∆ x quando ∆ xé1 ,0,5 ,0,1 ,0,01 ,0,001 , e∆ xé - 1 ,- 0,5 ,- 0,1 ,- 0,01 ,- 0,001 é é . A que f 2 + ∆ x - f ( 2 )

41) Dada f x = x - 3 Use uma calculadora para tabular valores de f 7 + ∆ x - f ( 7 ) ∆ x quando ∆ xé1 ,0,5 ,0,1 ,0,01 ,0,001 , e∆ xé - 1 ,- 0,5 ,- 0,1 ,- 0,01 ,- 0,001 é é . A que f 7 + ∆ x - f ( 7 )

42) Dada f x = 10 x 2 Use uma calculadora para tabular valores de f 5 + ∆ x - f ( 5 ) ∆ x quando ∆ xé1 ,0,5 ,0,1 ,0,01 ,0,001 , e∆ xé - 1 ,- 0,5 ,- 0,1 ,- 0,01 ,- 0,001 é é . A que f 5 + ∆ x - f ( 5 )