Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 18
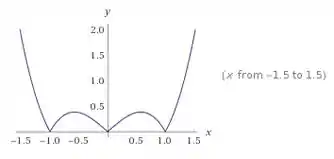
Construa uma função que seja contínua em e que seja derivável em todos os pontos, exceto em e .
Passo 1
Dos exercícios anteriores vimos que uma função derivável é aquela em que a função é suave, ou seja, aquela em que não apresenta um bico em seu esboço.
Passo 2
Um exemplo de função que seja derivável é um polinômio. Mas agora queremos que essa função não seja derivável em três pontos: . Bom, um polinômio de terceira ordem que corresponde a essas raízes seria um bom candidato. Mas e como deixar ele com um bico? Ah! É aqui que entra a função modular! Lembra que a função módulo deixa tudo que é negativo positivo? Então! Em um gráfico isso não é diferente!
Passo 3
Vamos supor o polinômio . Fatorando temos:
E as raízes () são . Dá uma espiada no gráfico:
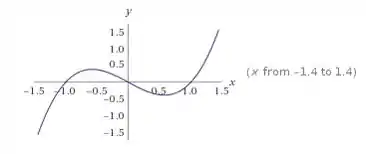
Super suave em todos os pontos, certo? Então temos que essa função é diferenciável em todos os pontos. Agora e se colocarmos um módulo nela? Sendo assim a nova função fica:
.
Toda a parte negativa passa para cima e ficamos com bicos justamente nas raízes dessa função. Saca só:
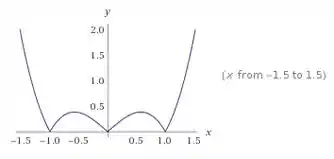
Beleza?
Resposta
