Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 11

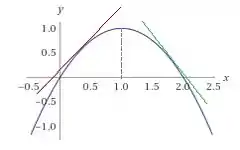
Dê exemplo (por meio de um gráfico) de uma função , definida e derivável em , tal que para , para .

Passo 1

Oi, galerinha! Tudo bom? O exercício pede um gráfico de uma função que tenha derivada positiva (reta tangente crescente) para e também tenha derivada negativa (reta tangente decrescente) para .

A ideia aqui é chutar uma função e ver se ela satisfaz essa condição!

Passo 2

Então minha escolha foi uma parábola com boca pra baixo e equação:

Com a ajuda de um programa de geração gráfica temos o esboço:

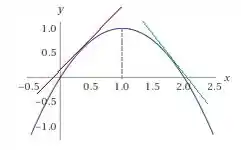
Aqui a reta tangente em vermelho representa a derivada da função antes do ponto de abcissa . Podemos ver que ela aponta para cima, ou seja, tem inclinação positiva. Enquanto que a reta tangente em verde representa a derivada da função depois de e aponta para baixo, ou seja, a derivada é negativa.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A área da região limitada pela curva y = e - x , pelos eixos coordenados e pela reta x =b (b0) é uma função de b. Se f for essa função , ache f(b). Ache também lim b → ∞ ⁡ f ( b )

O volume de um solido de revolução da região limitada pela curva y = e - x , pelos eixos coordenados e pela reta x =b (b0) é uma função de b. Se g for essa função , ache g(b). Ache também lim b → ∞ ⁡

Uma partícula move-se sobre uma reta , sendo s a distancia orientada da partícula a partir da origem , V m/s, a velocidade da partícula e A m/s² , a aceleração da partícula, t s. Se a = e t + e - t ,

Ache a equação da reta tangente à curva y = x x - 1 em (2,2)

Faça o Exercício 65 da série de Exercícios de Revisão do Capítulo 5, calculando todas as integrais.Exercício 65) Mostre que cada uma das desigualdades é válida: c ) ∫ 4 5 d x x - 3 ≥ ∫ 4 5 d x x