Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.8 - Ex. 18

Um tanque retangular aberto deve ter uma base quadrara e seu volume deve ser de 125   m ³ . O custo por metro quadrado é de $   24 para a base e de $   12 para os lados. Ache as dimensões do tanque cujo custo total do material seja mínimo.

Passo 1

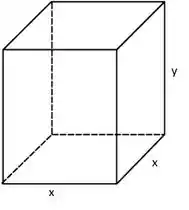
Seja x e y   as dimensões do nosso tanque, representado na figura abaixo. Sabemos que o volume do tanque é 125   m ³ . Vamos escrever a expressão que representa a área.

V = x ² y = 125   m 3 x ² y = 125 x ² y = 125 y = 125 x ²

Passo 2

A expressão que representa o custo do material será:

C = 24 x 2 + 12 * 4 x y = 24 x 2 + 48 x y Substituindo o valor de y na expressão acima temos:

C = 24 x 2 + 48 x * 125 x 2 C = 24 x 2 + 48 * 125 x C = 24 x 2 + 6000 x

Queremos que o custo seja mínimo. Para isso, vamos derivar a expressão acima em relação a x e igualar a zero.

d C d x = 0 = 48 x - 6000 x 6 0 00 x 2 = 48 x x 3 = 60 00 48 x 3 = 125 x = 5   m

Passo 3

Agora que encontramos o valor de y vamos substituir lá naquela expressão oriunda do volume, que encontramos no passo 1.

y = 125 5 y = 2 5   m

Resposta

Portanto, as dimensões do tanque são:

x = 5 m   e   y = 25   m

O custo mínimo será:

C = 24 * 5 2 + 48 * 5 * 25 C = 600 + 6000 C = $   6600

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está preparando um pôster retangular que deverá conter 50p o l . 2 de material impresso, com margens superior e inferir de 4p o l . Cada uma e margens à direita e À esquerda de 2p o l . cada uma
Um tanque retangular com 1125p ê s 2 ê de capacidade, de base quadrada, medindo x pés de lado e y pés de profundidade, será construído com a parte superior nivelada com o solo para captar água pluvial
Dois lados de um triângulo medem a e b , e o ângulo entre eles é de θ . Qual é o valor de θ que maximizará a área do triângulo.Dica: A = 1 2 a b sen ⁡ θ
Quais são as dimensões da lata mais leve em forma de cilindro reto, sem tampa, que pode conter 1000 c m 3 ? Compare o resultado com o exemplo 2
Você está projetando uma lata (um cilindro de revolução) de 1000c m 3 cuja manufatura levará em conta o desperdício. Não há desperdício ao cortar a lateral do alumínio, mas tanto a base como o topo, a