Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.Revisão - Ex. 104
Um tanque tem a forma de um sólido obtido ao girar a região limitada pela curva , pelo eixo e pelas retas e em torno do eixo . Se o tanque estiver cheio de água, qual o trabalho feito ao bombear toda água até a borda do tanque? A distância é medida em metros. Tome o eixo positivo vertical e orientado para baixo.
Passo 1
A questão pede para calcularmos o trabalho necessário para bombear toda a água de um tanque até a sua borda. O tanque é obtido pela rotação da região delimitada pela curva e as retas , e em torno do eixo . Uma visão em corte desse sólido é mostrada na figura a seguir:
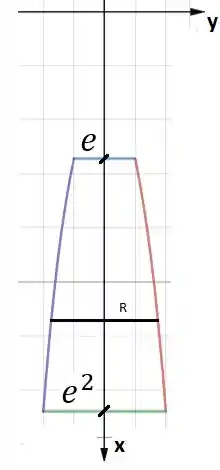
Para visualizar o sólido, pensa nessa figura rotacionada em torno do eixo . Assim, cada faixa horizontal do tanque será um disco de raio , como denotado na figura. Podemos escrever como função de :
Assim, a área de cada fatia (disco) será . Vamos considerar que cada uma dessas fatias tem uma espessura pequena , de modo que o volume de uma fatia localizada na posição vai ser
A massa de cada uma dessas fatias será
onde é a densidade da água.
O trabalho é o produto da força pelo deslocamento. No caso, a força é a força gravitacional, dada por
onde é a aceleração gravitacional. Para essa fatia localizada na posição , o deslocamento necessário para levá-la até a borda do tanque () será
Assim, o trabalho feito para essa fatia será
Portanto, o trabalho total será
Tomando o limite com , essa soma vira a integral:
Aqui acabou a parte de física e modelagem, agora é só cálculo!
Passo 2
Vamos reescrever a integral do trabalho como
Para calcular essa integral, vamos usar integração por partes:
Chamando e , temos que
Assim,
Assim,
Portanto,
Passo 3
Queremos calcular :
Para isso, vamos aplicar partes de novo com e :
Assim,
Portanto,
Logo,
Desta forma,
Assim, podemos achar :
Portanto,
Por fim, temos que
Usando e , obtemos