Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.7 - Ex. 3

Seja f x = x 2 + 1 x .

  1. Determine o ponto do gráfico de f em que a reta tangente, neste ponto, seja paralela ao eixo x .
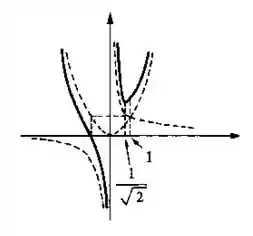
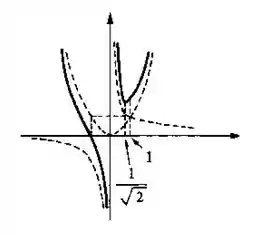
  2. Esboce o gráfico de f .

Passo 1

  1. Vamos lá, para encontrar esse ponto primeiro temos que encontrar a derivada da função f x , vamos analisar a função, é um polinômio, vamos ter que usar a fórmula da derivada de polinômio:

x n ' = n x n - 1

Agora é só aplicar, vamos lá?

f ' x = x 2 ' + 1 x ' = 2 x 2 - 1 + x - 1 ' = 2 x + - 1 ⋅ x - 1 - 1 = 2 x - x - 2 = 2 x - 1 x 2

Passo 2

E sabemos que o coeficiente angular m de uma reta é igual a derivada da função:

m = f ' x

Assim temos que para que a reta seja paralela ao eixo x , o coeficiente angular da reta deve ser igual a zero, ou seja, a derivada que acabamos de achar no passo anterior, vamos então igualar ela a zero, e temos a coordenada x do ponto que queremos:

2 x - 1 x 2 = 0 → 2 x 3 - 1 x 2 = 0 → 2 x 3 = 1 → x 3 = 1 2 → x = 1 2 3 = 1 2 3 = 1 2 3 ⋅ 2 3 2 3 ⋅ 2 3 2 3 = 4 3 2

Por último é só substituir na equação da reta para achar a coordenada y do ponto:

f 4 3 2 = 4 3 2 2 + 1 4 3 2 = 4 3 ⋅ 4 3 4 + 2 4 3 = 16 3 4 + 2 4 3 ⋅ 4 3 4 3 ⋅ 4 3 4 3 = 2 4 3 4 + 2 16 3 4 = 2 2 3 4 + 2 ⋅ 2 ⋅ 2 3 4 = 2 3 2 + 2 2 3 2 = 3 2 3 2

O ponto então é:

4 3 2 , 3 2 3 2

Passo 3

  1. Vamos esboçar o gráfico da função:

Resposta

  1. 4 3 2 , 3 2 3 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f x = sen ⁡ x , obtenha uma estimativa de f ' π 4 pelos seguintes métodos:Usando um recurso gráfico para fazer um zoom em um ponto apropriado do gráfico até que ele se pareça a uma reta e, então,
Suponha que o custo da perfuração de x metros para um poço de petróleo seja de C = f x dólares.Quais são as unidades de f ' x ?Em termos práticos, qual é o significado de f ' x neste caso?O que pode s
Encontre d y d x | x = 1 , sabendo que y = 1 - x 2 .
Uma empresa fabricante de tintas estima que pode vender g = f p galões de tinta a um preço de p reais.Quais são as unidades de d g g p ?Em termos práticos, o que significa d g d p neste caso?O que pod
O limite dado representa f ' a para alguma função f e algum número a . Encontre f x e a em cada caso. lim h → 0 ⁡ cos ⁡ π + h + 1 h lim x → 1 ⁡ x 7 - 1 x - 1