A temperatura de uma localidade do Hemisfério Norte depende da longitude , da latitude e do tempo , de modo que podemos escrever . Vamos medir o tempo em horas a partir do início de janeiro.

(a) Qual é o significado das derivadas parciais , e ?

(b) Honolulu tem longitude de 158°W e latitude de 21°N. Suponha que às 9 horas em 1º de janeiro esteja ventando para nordeste uma brisa quente, de forma que a oeste e a sul o ar esteja quente e a norte e leste o ar esteja mais frio. Você esperaria que , e fossem positivas ou negativas? Explique.

O objetivo no item (a) é interpretar o significado físico da derivada parcial de uma função em relação a uma variável, e sabemos que pelo conceito de derivadas parciais, apenas a variável da derivação é levada em consideração (as demais são tratadas como constante). Dessa forma podemos descrever que:

É a taxa de variação da temperatura quando apenas (a longitude) varia.

É a taxa de variação da temperatura quando apenas (a latitude) varia.

É a taxa de variação da temperatura quando apenas t (o tempo) varia.

Depois disso, no item (b), temos uma situação que pode ser descrita de forma pelo esquema:

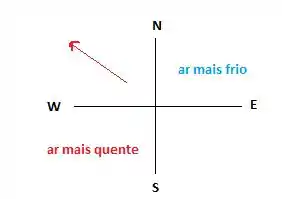
Quando apenas a longitude varia, temos positivo: conforme aumentamos a longitude seguindo a oeste, a temperatura aumenta.

Quando apenas a latitude varia, temos negativo, pois, ao aumentarmos a latitude seguindo a norte, a temperatura diminui.

E, finalmente, quando apenas o tempo varia, temos positivo, pois a brisa é quente e com o passar do tempo, a temperatura aumenta.