Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 3
O índice de sensação térmica é a temperatura percebida quando a temperatura real é e a velocidade do vento é , de modo que podemos escrever . A tabela de valores a seguir é um trecho da tabela 1 da seção 14.1.
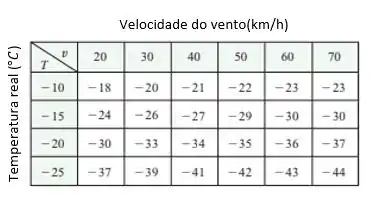
a) Estime os valores de e Quais são as interpretações práticas desses valores?
b) Em geral, o que você pode dizer sobre os sinais de e ?
c) Qual parece ser o valor do seguinte limite?
Passo 1
E aí, pessoal! Tudo bem?
Nessa questão nós temos uma tabela de temperatura real versus velocidade do vento. Cada interseção entre uma linha e uma coluna corresponde ao valor do índice de sensação térmica para um ponto .
No item a), vamos pensar na definição de derivadas por limites para fazer a estimativa de e . Temos que lembrar que para calcular nós fixamos e variamos . Matematicamente, escrevemos:
Então, para calcular e , vamos fixar o ponto e fazer a menor variação possível em e respectivamente.
No item b), para responder sobre o sinal das derivadas de nós vamos analisar a função.
Por fim, no item c), vamos analisar o que acontece com a derivada de com respeito a .
Passo 2
No item a), inicialmente é importante saber a interpretação das seguintes derivadas parciais e . A primeira representa a variação da temperatura quando fixamos a velocidade do vento em 30 km/h, enquanto a segunda representa a variação da velocidade quando fixamos a Temperatura real em 30 graus.
Para estimar os valores, é possível fazer uma média a partir dos valores dados na tabela.
Ao estimar , fixamos a velocidade do vento e vemos a variação da sensação térmica com o aumento da temperatura de -15 graus para -10 graus.
Assim,
=
Isto é, ao aumentarmos a temperatura, também ocorre um aumento na sensação térmica.
Ao estimar , fixamos a temperatura e vemos a variação da sensação térmica com o aumento da velocidade do vento de 30 km/h para 40 km/h.
Assim,
= = - 0,1
Isto é, ao aumentarmos a velocidade do vento, ocorre uma diminuição na sensação térmica.
Passo 3
Agora vamos responder o item b):
Em geral, podemos dizer que se fixamos e aumentamos, a sensação térmica diminui, ou seja, é negativo. Todavia, quando fixamos e aumentamos , a sensação térmica aumenta, ou seja, é positivo.
Passo 4
De acordo com a tabela, ao fixar o valor de e aumentar o valor de, observa-se uma tendência de uma sensação térmica constante para cada analisado. Ou seja, a taxa de variação da sensação térmica tende a zero. Portanto:
Resposta
- = . Isto é, ao aumentarmos a temperatura, também ocorre um aumento na sensação térmica. = - 0,1. Isto é, ao aumentarmos a velocidade do vento, ocorre uma diminuição na sensação térmica.
- Se fixamos e aumentamos : é negativo.Quando fixamos e aumentamos : é positivo.