Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.1 - Ex. 41
Use um gráfico da sequência para decidir se a sequência é convergente ou divergente. Se a sequência for convergente, estime o valor do limite a partir do gráfico e então prove sua estimativa. (Veja a margem esquerda na página com sugestões para gráficos de sequências).
41-
Passo 1
Vamos entender o que a questão pede: o gráfico da sequência vai nos mostrar o comportamento de seus valores ao longo dos termos da sequência. Precisamos então plotar esse gráfico e analisar se a sequência se aproxima de algum valor conforme os valores de vão crescendo.
Caso haja a convergência da sequência, podemos provar nossa estimativa calculando .
Passo 2
Agora precisamos de fato plotar o gráfico e para isso podemos recorrer ao software GeoGebra.
Nesse software utilizamos a função “sequência”, com variando entre 1 e 100. Os 100 primeiros são suficientes para notarmos o padrão que a sequência vai seguir.
O gráfico plotado pelo software é:
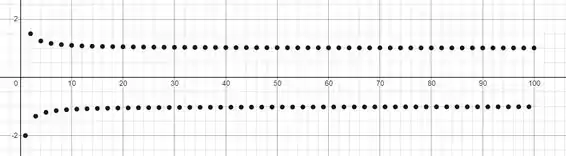
Onde à medida que vamos aumentando o valor de , o gráfico fica oscilando entre e e por isso dizemos que a sequência diverge. Isso pode soar estranho pois a divergência na nossa cabeça parece que só ocorre quando a sequência tende a um valor infinito, mas nem sempre é assim. A oscilação entre dois valores também é uma divergência.
Essa oscilação pode ser notada mesmo se não tivéssemos o gráfico, pelo termo presente na nossa sequência. Quando é ímpar, esse termo fica negativo e quando é par esse termo fica positivo. Dessa forma ele vai sempre alternando o sinal da nossa expressão.
Resposta
A sequência é divergente.