Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 35
35. para todos os reais? Justifique sua resposta.
Passo 1
A função piso representa o maior número inteiro menor ou igual a . E a função teto representa o menor número inteiro maior ou igual a . Ou seja em uma a gente arredonda o número para cima e na outra a gente arredonda o número para baixo.
Para esse caso o mais fáci é a gente montar um pedaço do gráfico que dai a gente percebe que eles sempre vão ser iguais:
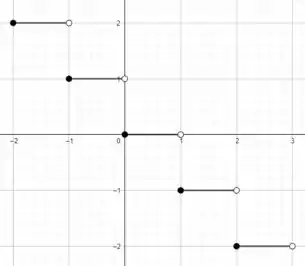
Passo 2
Agora que a gente imagina que eles são iguais temos que tentar provar. Então precisamos pegar valores quaisquer para , para poder substituir na equação e tentar chegar em uma igualdade.
Se a gente pegar um qualquer:
Essa inequação quer dizer que está entre dois inteiros quaisquer.
Para esse caso:
Passo 3
Já temos , agora precisamos encontrar . Então vamos multiplicar a inequação de antes por , dessa forma a gente consegue ter o :
Aplicando a função teto:
Passo 4
Então é só substituir na equação:
para todo .
Resposta
Ei, a resposta está no passo a passo :)