Um objeto com massa é arrastado ao longo de um plano horizontal por uma força agindo ao longo de uma corda presa ao objeto. Se a corda faz um ângulo com o plano, então a intensidade da força é
Onde é uma constante positiva chamada coeficiente de atrito e . Mostre que é minimizada quando .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer que a gente encontre o menor valor possível para a força , quando .
Pra isso, ele nos disse que o objeto de massa é arrastado ao longo de um plano horizontal por um força de intensidade:
Onde é uma constante positiva chamada coeficiente de atrito e .
Sendo assim, vamos usar os conceitos de máximo e mínimo aqui, beleza? Lembrando que os pontos críticos de uma função são os valores de nos quais a derivada da função é igual a zero ou não está definida.
Então, seja . Agora, calcularemos a derivada de em relação ao ângulo e igualaremos a zero para encontrar os pontos críticos.
Vamos lá!
Passo 2
Derivando a equação da força:
Igualando a zero para que encontremos os pontos críticos:
Para continuarmos deveremos aplicar o método do invervalo fechado:
O Método do Intervalo Fechado - Para encontrar os valores máximo e mínimo absolutos de uma função contínua f em um intervalo fechado [a,b]:
1- Encontre os valores de f nos extremos do intervalo.
2- Encontre os valores de f nos números críticos de f em [a,b].
3- O maior valor das etapas 1 e 2 é o valor máximo absoluto, ao passo que o menor desses valores é o valor mínimo absoluto.
Passo 3
Agora, necessitamos aplicar o teorema do intervalo fechado, então, precisamos calcular o valor da força quando . Substituindo isso na fórmula de :
Arrumando:
Então, esse é o valor de quando , beleza? Falta só saber quanto é .
Passo 4
Bom, então, vamos descobrir o valor de . Para isso, vamos montar um triângulo retângulo com as informações que sabemos sobre . Sabemos que , então podemos desenhar o seguinte triângulo retângulo:
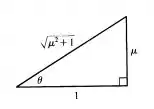
Onde é a hipotenusa desse triângulo, que achamos usando Pitágoras, ok?
Daí, tiramos que
Então, substituindo esse valor na que achamos no passo anterior
Agora sim, esse será nosso valor da quando .
Você pode reparar que aqui , então, nosso termo:
Opa, ele será um valor positivo, mas menor que 1. E quando multiplicamos algo por um valor entre e , o produto é um número menor. No nosso caso:
Além disso, geralmente, os valores de coeficiente de atrito são maiores que 1, então:
Beleza? Vamos usar essas análises no passo seguinte.
Passo 5
Agora, pelo teorema do intervalo fechado, necessitamos calcular e
Opa, e como vimos anteriormente:
Então, quando temos que e este é o menor valor possível para .
Prontinho!! Provado. 😊