Traçar o gráfico das funções trigonométricas. Comparar cada conjunto identificando a transformação ocorrida. Identificar domínio, conjunto imagem, máximos e mínimos, crescimento e decrescimento.
e)
Passo 1
Então pessoal, de início vamos plotar o gráfico das funções e que nos foram dadas, tudo bem? A é uma função seno bem conhecida, a é a mesma função, mas refletida em torno do eixo devido ao sinal de negativo. Para confirmarmos:
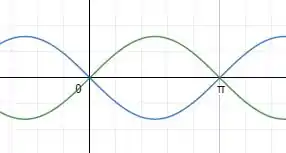
No qual a função em verde é ;
A função em azul é .
Passo 2
Para facilitar a nossa análise, como são vários pontos para analisar vamos pontuar um de cada vez, tudo bem? Algo muuuuito importante de ser ressaltado aqui, galera, é que os resultados para sempre serão opostos aos de , também devido ao sinal negativo. Em outras palavras, o mínimo de será o máximo de , o intervalo de crescimento de será o intervalo de decrescimento de e assim por diante. Para confirmar:
- Transformações ocorridas:
- Domínio:
- Imagem:
- Máximos:
- Mínimos:
- Intervalos de crescimento:
- Intervalos de decrescimento:
Assim como já descrito no passo , de para houve uma reflexão em torno do eixo devido ao sinal negativo que aparece na função !
Então pessoal, para a variável independente que temos não há nenhuma restrição, pode assumir qualquer valor, seja em ou em , logo:
A imagem da função seno é bem conhecida, assim como as imagens das funções cosseno e tangente, uma vez que são bem limitadas! Sabemos que as funções seno e cosseno possuem a mesma imagem, são funções que variam de a , não é mesmo? Sendo assim, teremos:
Passo 3
Agora vamos determinar os máximos e mínimos e os intervalos de crescimento e decrescimento das funções:
A função seno é máxima quando vale , não é mesmo? Isso acontece em para e em para , logo:
Assim como comentado no passo , as funções são opostas, então teremos que os pontos de mínimo de serão os pontos de máximo de e vice-versa, se liga:
Os intervalos de crescimento ocorrem quando a função está atingindo seu ponto de máximo, que no caso da nossa função é em . Sendo assim, os intervalos serão em:
Assim como comentado no passo , as funções são opostas, então teremos que os intervalos de decrescimento de serão os intervalos de crescimento de e vice-versa, saca só:
Aqui vale ressaltar que é uma constante inteira, tudo bem? Foi demorado, mas está aí nossa análise completa! 😊
Resposta
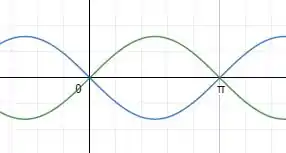
Domínio e imagem:
Máximos e mínimos:
Intervalos de crescimento e decrescimento: